
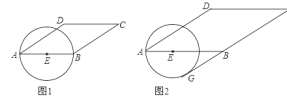
【题目】如图,在平行四边形ABCD中,AB=10(AB>AD),AD与BC之间的距离为6,点E在线段AB上移动,以E为圆心,AE长为半径作⊙E.
(1)如图1,若E是AB的中点,求⊙E在AD所在的直线上截得的弦长;
(2)如图2,若⊙E与BC所在的直线相切,求AE的长.
【答案】(1)AF=8;(2)AE=![]() .
.
【解析】
(1)设AD和圆相交于F,连接BF,由圆周角定理可得BF⊥AD,所以BF=8,根据勾股定理即可求出AF的长;
(2)过点B作BM⊥AD于点M,连接EF.利用平行线AD∥CB的性质推知内错角∠DAB=∠ABM;然后在Rt△ABM和Rt△BEG中根据三角函数的定义求得比例式,利用比例的性质即可求得AE的值.
解:(1)设AD和圆相交于F,连接BF,
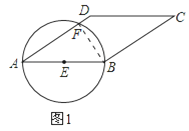
∵AB是圆的直径,
∴∠AFB=90°,
∴BF⊥AD,
∵AD与BC之间的距离为6,
∴BF=6,
∴AB=10,
∴AF=![]() =8;
=8;
(2)过点B作BM⊥AD于点M,连接EG.
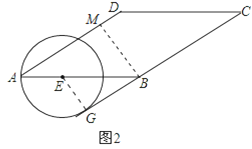
∵AD与BC之间的距离为6,
∴BM=6;
∴sin∠DAB=![]() =
=![]() ;
;
又∵CG是⊙E的切线,
∴EG⊥CG,
∴cos∠BEG=![]() ;
;
∵四边形ABCD是平行四边形,
∴AD∥BC(平行四边形的对边相互平行),
∴∠DAB=∠ABG(两直线平行,内错角相等);
∵AE=EG(⊙E的半径),
∴![]()
即![]() ,
,
∴AE=![]() .
.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】莲城超市以10元/件的价格调进一批商品,根据前期销售情况,每天销售量y(件)与该商品定价x(元)是一次函数关系,如图所示.
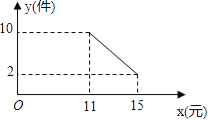
(1)求销售量y与定价x之间的函数关系式;
(2)如果超市将该商品的销售价定为13元/件,不考虑其它因素,求超市每天销售这种商品所获得的利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上一个动点,过点
边上一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平分线于点
的平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
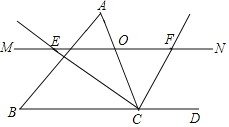
(1)探究![]() 与
与![]() 的数量关系并加以证明;
的数量关系并加以证明;
(2)当点![]() 运动到
运动到![]() 上的什么位置时,四边形
上的什么位置时,四边形![]() 是矩形,请说明理由;
是矩形,请说明理由;
(3)在(2)的基础上,![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?为什么?
是正方形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
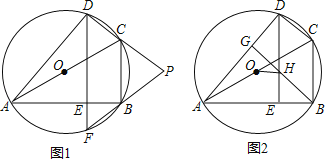
【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0;②当-1≤x≤3时,y<0;③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2;④9a+3b+c=0,其中正确的是( )
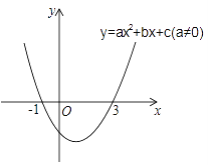
A. ①②③ B. ①②④ C. ①④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 分别在菱形
分别在菱形![]() 的边
的边![]() 上滑动(点
上滑动(点![]() 不与
不与![]() 重合),且
重合),且![]() .
.
(1)如图1,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() 与
与![]() 不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
不垂直,(1)中的结论还成立吗?若成立,请证明,若不成立,说明理由;
(3)如图3,若![]() ,请直接写出四边形
,请直接写出四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量校园内一棵大树的高度,学校数学应用实践小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计了如图的测量方案,把镜子放在离树(AB)8.7m的点E处,然后沿直线BE后退到点D,这时恰好在镜子里看到树顶点A,再用皮尺测量得DE=2.7m,观察者眼睛距地面的高CD=1.6m,请你计算树(AB)的高度.(精确到0.1m)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com