
【题目】将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A( ![]() ,0),点B(0,1),点0(0,0).过边OA上的动点M(点M不与点O,A重合)作MN丄AB于点N,沿着MN折叠该纸片,得顶点A的对应点A′,设OM=m,折叠后的△AM′N与四边形OMNB重叠部分的面积为S.
,0),点B(0,1),点0(0,0).过边OA上的动点M(点M不与点O,A重合)作MN丄AB于点N,沿着MN折叠该纸片,得顶点A的对应点A′,设OM=m,折叠后的△AM′N与四边形OMNB重叠部分的面积为S.
(1)如图①,当点A′与顶点B重合时,求点M的坐标;
(2)如图②,当点A′,落在第二象限时,A′M与OB相交于点C,试用含m的式子表示S;
(3)当S= ![]() 时,求点M的坐标(直接写出结果即可).
时,求点M的坐标(直接写出结果即可).
【答案】
(1)
解:在Rt△ABO中,点A( ![]() ,0),点B(0,1),点O(0,0),
,0),点B(0,1),点O(0,0),
∴OA= ![]() ,OB=1,
,OB=1,
由OM=m,可得:AM=OA﹣OM= ![]() ﹣m,
﹣m,
根据题意,由折叠可知△BMN≌△AMN,
∴BM=AM= ![]() ﹣m,
﹣m,
在Rt△MOB中,由勾股定理,BM2=OB2+OM2,
可得: ![]() ,解得m=
,解得m= ![]() ,
,
∴点M的坐标为( ![]() ,0);
,0);
(2)
解:在Rt△ABO中,tan∠OAB= ![]() ,
,
∴∠OAB=30°,
由MN⊥AB,可得:∠MNA=90°,
∴在Rt△AMN中,MN=ANsin∠OAB= ![]() ,
,
AN=ANcos∠OAB= ![]() ,
,
∴ ![]() ,
,
由折叠可知△A'MN≌△AMN,则∠A'=∠OAB=30°,
∴∠A'MO=∠A'+∠OAB=60°,
∴在Rt△COM中,可得CO=OMtan∠A'MO= ![]() m,
m,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
即 ![]() ;
;
(3)
解:①当点A′落在第二象限时,把S的值代入(2)中的函数关系式中,解方程求得m,根据m的取值范围判断取舍,两个根都舍去了;
②当点A′落在第一象限时,则S=SRt△AMN,根据(2)中Rt△AMN的面积列方程求解,根据此时m的取值范围,把S= ![]() 代入,可得点M的坐标为(
代入,可得点M的坐标为( ![]() ,0).
,0).
【解析】(1)根据折叠的性质得出BM=AM,再由勾股定理进行解答即可;(2)根据勾股定理和三角形的面积得出△AMN,△COM和△ABO的面积,进而表示出S的代数式即可;(3)把S= ![]() 代入解答即可.
代入解答即可.
【考点精析】关于本题考查的翻折变换(折叠问题),需要了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,连AD,BE,F为线段AD的中点,连接CF
(1)如图1,当D点在BC上时,求证:①BE=2CF,②BE⊥CF.
(2)如图2,把△DEC绕C点顺时针旋转一个锐角,其他条件不变,问(1)中的关系是否仍然成立?如果成立请证明.如果不成立,请写出相应的正确的结论并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖. 
(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac﹣b2<0.其中正确结论有 . 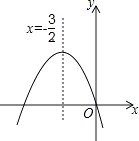
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写如表:
蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
所付的金额(元) | … | 125 | 300 | … |
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式; 
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个构造完全相同(除所标数字外)的转盘A、B,游戏规定:转动两个转盘各一次,指向大的数字获胜.
(1)用树状图或列表格列出两个转盘转出的所有可能出现的结果;
(2)如果由你和小明各选择一个转盘游戏,你会选择哪一个,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司引进A、B两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,根据图象提供的信息,解答下列问题: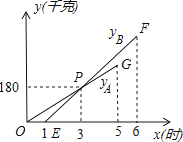
(1)求yB关于x的函数解析式;
(2)如果A、B两种机器人连续搬运5个小时,那么B种机器人比A种机器人多搬运了多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠A=30°,点D,E分别在边AC,AB上,点D与点A,点C都不重合,点F在边CB的延长线上,且AE=ED=BF,连接DF交AB于点G.若BC=4,则线段EG的长为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com