
分析 (1)根据数的乘方,根式的性质化简即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)(-2)3×$\sqrt{(-4)^{2}}$+$\root{3}{(-4)^{3}}$×($\frac{1}{2}$)2-$\sqrt{9}$=-8×4-4×$\frac{1}{4}$-3=-36;
(2)①$\left\{\begin{array}{l}{x-y=1①}\\{2x+y=2②}\end{array}\right.$,
①+②得,3x=3,
∴x=1,
把x=1代入①得,y=0,
∴$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$;
②$\left\{\begin{array}{l}{x-3y=1①}\\{2x+y-15=1②}\end{array}\right.$,
①+②×3得,x=7,
把x=7代入①得,y=2,
∴$\left\{\begin{array}{l}{x=7}\\{y=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,实数的运算,利用了消元的思想,消元的方法有:代入消元法与加减消元法.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
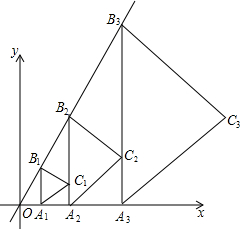 如图,点A1(1,0)在x轴上,过点A1作A1B1∥y轴交直线y=$\sqrt{3}$x于点B1,以A1B1为边在A1B1的右侧作等边△A1B1C1,再过点C1作A2B2∥y轴,分别交直线x轴和直线y=$\sqrt{3}$x于A2,B2两点,再以A2B2为边在A2B2的右侧作等边△A2B2C2…,按此规律进行下去,则等边△AnBnCn的面积为$\frac{\sqrt{3}}{4}$[$(\frac{5}{2})^{n-1}$•$\sqrt{3}$]2(用含正整数n的代数式表示).
如图,点A1(1,0)在x轴上,过点A1作A1B1∥y轴交直线y=$\sqrt{3}$x于点B1,以A1B1为边在A1B1的右侧作等边△A1B1C1,再过点C1作A2B2∥y轴,分别交直线x轴和直线y=$\sqrt{3}$x于A2,B2两点,再以A2B2为边在A2B2的右侧作等边△A2B2C2…,按此规律进行下去,则等边△AnBnCn的面积为$\frac{\sqrt{3}}{4}$[$(\frac{5}{2})^{n-1}$•$\sqrt{3}$]2(用含正整数n的代数式表示).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
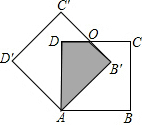 如图,边长为1的正方形ABCD中绕点A逆时针旋转30°得到正方形AB′C′D′,则图中阴影部分的面积为$\frac{{\sqrt{3}}}{3}$.
如图,边长为1的正方形ABCD中绕点A逆时针旋转30°得到正方形AB′C′D′,则图中阴影部分的面积为$\frac{{\sqrt{3}}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
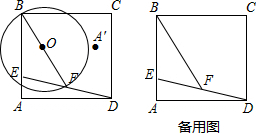
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com