
【题目】如图,△ ABC中,∠ ABC=90°,AB=BC,D在边 AC上,AE┴ BD于 E.

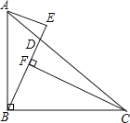
(1) 如图 1,作 CF⊥ BD于 F,求证:CF-AE=EF;
(2) 如图 2,若 BC=CD,求证:BD=2AE ;
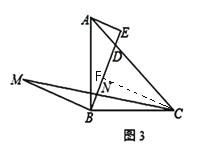
(3) 如图3,作 BM ⊥BE,且 BM=BE,AE=2,EN=4,连接 CM交 BE于 N,请直接写出△BCM的面积为______.
【答案】(1)见解析;(2)见解析;(3)5.
【解析】
(1)根据已知条件证明△ABE≌△BCF,即可求解;
(2)过点C作 CF⊥BD于点F,由(1)可知AE=BF=DF,故可求解;
(3)过点C作 CF⊥BD于点F,由(1)得△ABE≌△BCF,再证△BMN≌△FCN,根据S△BCM= S△BCN+S△MBN = S△BCN+S△CFN= S△BCM=![]() 即可求解.
即可求解.
(1) 证明:∵CF⊥BD于点F,AE⊥BD,
∴∠AEB=∠CFB=90°,
∴∠ABE+∠BAE=90°,
又∵∠ABC=90°,
∴∠ABE+∠CBF=90°,
∴∠BAE=∠CBF,
在![]() 中,
中,
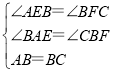
∴△ABE≌△BCF(AAS),
∴BE=CF,AE=BF,
∴CF-AE= BE-BF=EF.
(2)过点C作 CF⊥BD于点F,
∵BC=CD
∴BF=DF
由(1)得AE=BF,
∴AE=DF
∴BD=2AE
(3) 由(1)得△ABE≌△BCF
∵BM=BE
∴BM=CF
∵BM ⊥BE,∴∠MBN=∠CFN
又∠MNB=∠CNF
∴△BMN≌△FCN,∴BN=FN
∵AE=2,EN=4,
∴BF=AE=2,BN=![]() BF=1
BF=1
故BE=5,
∴S△BCM= S△BCN+S△MBN = S△BCN+S△CFN=![]()


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图所示,AD是△ABC的中线,AE⊥AB,AF⊥AC,且AE=AB,AF=AC,AD=3,AB=4.

(1)求AC长度的取值范围;
(2)求EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD,
求证:∠EGF=90°.
证明:∵AB∥GH(已知),
∴∠1=∠3( ),
又∵CD∥GH(已知),
∴ (两直线平行,内错角相等)
∵AB∥CD(已知),
∴∠BEF+ =180°(两直线平行,同旁内角互补)
∵EG平分∠BEF(已知),
∴∠1=![]() (角平分线定义),
(角平分线定义),
又∵FG平分∠EFD(已知),
∴∠2=![]() ∠EFD( ),
∠EFD( ),
∴∠1+∠2=![]() ( +∠EFD)
( +∠EFD)
∴∠l+∠2=90°,
∴∠3+∠4=90°(等量代换),
即∠EGF=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大树AB与大数CD相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为90°,且EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,小华行走到点E的时间是( )

A. 13s B. 8s C. 6s D. 5s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC和△CDE都是等边三角形,且A、C、E三点共线.AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:① AD=BE;② ∠AOB=60°;③AP=BQ; ④△PCQ是等边三角形;⑤PQ∥AE.其中正确结论的有( )个

A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
A. 有两边和其中一边的对角对应相等的两个三角形全等
B. 两条平行直线被第三条直线所截,则一组同旁内角的平分线互相垂直
C. 三角形的一个外角等于两个内角的和
D. 等边三角形既是中心对称图形,又是轴对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为m的正方形面积为12,则下列关于m的说法中:①m2是有理数;②m的值满足m2﹣12=0;③m满足不等式组![]() ;④m是12的算术平方根. 正确有几个( )
;④m是12的算术平方根. 正确有几个( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区的三个景点A、B、C在同一线路上.甲、乙两名游客从景点A出发,甲步行到景点C;乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C,甲、乙两人同时到达景点C.甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示.

(1)乙步行的速度为_ __米/分.
(2)求乙乘景区观光车时y与x之间的函数关系式.
(3)甲出发多长时间与乙第一次相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com