
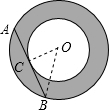
 有人请泰克地毯公司为某新建机场的环形通道铺设地毯.当泰克先生拿到计划蓝图(如图)时,他有些生气:与内圆相切的一条弦的长度是唯一给出的尺寸数据.“这就难了,”泰克想,“两圆之间环形阴影的面积不知道,怎么能估计出大致需要多少地毯呢?最好去找找设计师萨普先生.”萨普先生是个优秀的几何学家,他对此倒是处之泰然:“对我来说,有这一个数据就够了,把这个数据代入公式就能求出圆环的面积.”泰克先生吃了一惊,略一思索,便现出了笑容:“谢谢你,萨普先生,无须劳驾你动用什么公式了,我可以马上得出答案.”你知道泰克先生是怎么算的吗?
有人请泰克地毯公司为某新建机场的环形通道铺设地毯.当泰克先生拿到计划蓝图(如图)时,他有些生气:与内圆相切的一条弦的长度是唯一给出的尺寸数据.“这就难了,”泰克想,“两圆之间环形阴影的面积不知道,怎么能估计出大致需要多少地毯呢?最好去找找设计师萨普先生.”萨普先生是个优秀的几何学家,他对此倒是处之泰然:“对我来说,有这一个数据就够了,把这个数据代入公式就能求出圆环的面积.”泰克先生吃了一惊,略一思索,便现出了笑容:“谢谢你,萨普先生,无须劳驾你动用什么公式了,我可以马上得出答案.”你知道泰克先生是怎么算的吗?| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
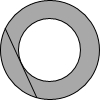 有人请泰克地毯公司为某新建机场的环形通道铺设地毯.当泰克先生拿到计划蓝图(如图)时,他有些生气:与内圆相切的一条弦的长度是唯一给出的尺寸数据.“这就难了,”泰克想,“两圆之间环形阴影的面积不知道,怎么能估计出大致需要多少地毯呢?最好去找找设计师萨普先生.”萨普先生是个优秀的几何学家,他对此倒是处之泰然:“对我来说,有这一个数据就够了,把这个数据代入公式就能求出圆环的面积.”泰克先生吃了一惊,略一思索,便现出了笑容:“谢谢你,萨普先生,无须劳驾你动用什么公式了,我可以马上得出答案.”你知道泰克先生是怎么算的吗?
有人请泰克地毯公司为某新建机场的环形通道铺设地毯.当泰克先生拿到计划蓝图(如图)时,他有些生气:与内圆相切的一条弦的长度是唯一给出的尺寸数据.“这就难了,”泰克想,“两圆之间环形阴影的面积不知道,怎么能估计出大致需要多少地毯呢?最好去找找设计师萨普先生.”萨普先生是个优秀的几何学家,他对此倒是处之泰然:“对我来说,有这一个数据就够了,把这个数据代入公式就能求出圆环的面积.”泰克先生吃了一惊,略一思索,便现出了笑容:“谢谢你,萨普先生,无须劳驾你动用什么公式了,我可以马上得出答案.”你知道泰克先生是怎么算的吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com