
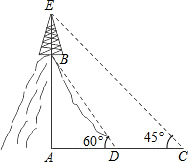
 如图,在山顶有座移动通信发射塔BE,高为30米.为了测量山高AB,在地面引一基线ADC,测得∠BDA=60°,∠C=45°,DC=40米,求山高AB.(不求近似值)
如图,在山顶有座移动通信发射塔BE,高为30米.为了测量山高AB,在地面引一基线ADC,测得∠BDA=60°,∠C=45°,DC=40米,求山高AB.(不求近似值)  百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
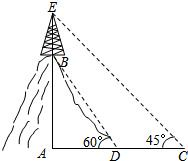 如图,在山顶有座移动通信发射塔BE,高为30米.为了测量山高AB,在地面引一基线ADC,测得∠BDA=60°,∠C=45°,DC=40米,则山高AB=
如图,在山顶有座移动通信发射塔BE,高为30米.为了测量山高AB,在地面引一基线ADC,测得∠BDA=60°,∠C=45°,DC=40米,则山高AB=查看答案和解析>>
科目:初中数学 来源:第7章《锐角三角函数》中考题集(42):7.6 锐角三角函数的简单应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第1章《解直角三角形》中考题集(39):1.3 解直角三角形(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第21章《解直角三角形》中考题集(36):21.5 应用举例(解析版) 题型:解答题
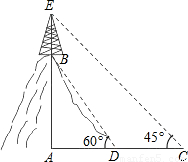
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com