Question

8．如图，抛物线y=ax²-3ax-2与x轴交于A、B，与y轴交于C，连AC、BC，∠ABC=∠ACO．
（1）求抛物线的解析式．
（2）设P为线段OB上一点，过P作PN∥BC交OC于N，设线PN为y=kx+m，将△PON沿PN折叠，得△PNM，点M恰好落在第四象限的抛物线上，求m的值．
（3）CE平分∠ACB交抛物线的对称轴于E，连AE，在抛物线上是否存在点P，使∠APC＞∠AEC，若存在，求出点P的横坐标x_p的取值范围，若不存在，请说明理由．

Answer 1

分析 （1）如图1中，由△AOC∽△COB，得$\frac{OA}{CO}$=$\frac{CO}{OB}$，得OA•OB=OC²=4，结合根与系数关系即可解决问题．
（2）如图2中，首先证明OM⊥BC，求出直线OM的解析式，利用方程组求出点M坐标，再求出PN的解析式即可解决问题．
（3）如图3中，CE交AB于M，作MG⊥AC于G，MH⊥BC于H，连接EB．对称轴与x轴交于点K．首先证明E、A、C、B四点共圆，圆心为K，⊙K与抛物线在第四象限的交点为F．观察图象即可解决问题．

解答 解：（1）如图1中，设A（m，0），B（n，0），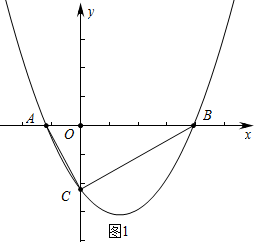

∵∠ACO=∠CBO，∠AOC=∠BOC=90°，
∴△AOC∽△COB，
∴$\frac{OA}{CO}$=$\frac{CO}{OB}$，
∴OA•OB=OC²=4，
∴$\frac{-2}{a}$=-4，
∴a=$\frac{1}{2}$，
∴抛物线解析式为y=$\frac{1}{2}$x²-$\frac{3}{2}$x-2．

（2）如图2中，PN与OM交于点G，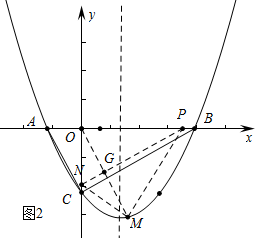

由题意OM⊥PN，
∵PN∥BC，
∴OM⊥BC，
∵直线BC的解析式为y=$\frac{1}{2}$x-2，
∴直线OM的解析式为y=-2x，
由$\left\{\begin{array}{l}{y=-2x}\\{y=\frac{1}{2}{x}^{2}-\frac{3}{2}x-2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{-1+\sqrt{17}}{2}}\\{y=1-\sqrt{17}}\end{array}\right.$，或$\left\{\begin{array}{l}{x=\frac{-1-\sqrt{17}}{2}}\\{y=1+\sqrt{17}}\end{array}\right.$，
∴点M坐标（$\frac{-1+\sqrt{17}}{2}$，1-$\sqrt{17}$），
∵OG=GM，
∴点G坐标（$\frac{-1+\sqrt{17}}{4}$，$\frac{1-\sqrt{17}}{2}$），
∴直线PN的解析式为y=$\frac{1}{2}$x+$\frac{5-5\sqrt{17}}{8}$，
∴m=$\frac{5-5\sqrt{17}}{8}$．

（3）如图3中，CE交AB于M，作MG⊥AC于G，MH⊥BC于H，连接EB．对称轴与x轴交于点K．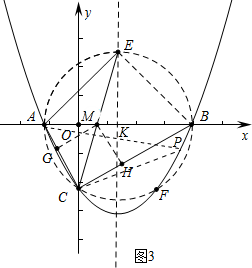

∵CE平分∠ACB，
∴MG=MH，
∵A（-1，0），B（4，0），C（0，-2）
∴AC=$\sqrt{5}$，BC=2$\sqrt{5}$，AB=5，
∴$\frac{{S}_{△ACM}}{{S}_{△BCM}}$=$\frac{AM}{BM}$=$\frac{\frac{1}{2}•AC•MG}{\frac{1}{2}•BC•MH}$=$\frac{AC}{BC}$=$\frac{\sqrt{5}}{2\sqrt{5}}$
∴AM=$\frac{5}{3}$，OM=$\frac{2}{3}$，
∴直线CE解析式为y=3x-2，
∴点E坐标（$\frac{3}{2}$，$\frac{5}{2}$），
∴EK=AK=KB，
∴△EAB是等腰直角三角形，
∴∠EBA=∠ACE=45°，
∴E、A、C、B四点共圆，圆心为K，⊙K与抛物线在第四象限的交点为F．
根据对称性，点F坐标（3，-2），
由图象可知，当点P在抛物线A→C段或B→F段时，∠APC＞∠AEC，
此时点P的横坐标x_p的取值范围-1＜x_P＜0或3＜x_P＜4．

点评 本题考查二次函数综合题、一次函数、角平分线的性质、相似三角形的判定和性质、四点共圆等知识，解题的关键是灵活应用这些知识解决问题，学会利用方程组确定两个函数的交点坐标，第三个问题的突破点是利用圆，找到点P的位置，属于中考压轴题．