Question

2．如图所示，在△ABC中，BC=4，E、F分别是AB、AC上的点，且EF∥BC，动点P在射线EF上，BP交CE于点D，∠CBP的平分线交CE于Q，当CQ=$\frac{1}{3}$CE时，EP+BP=8．

Answer 1

分析 如图，延长EF交BQ的延长线于G．首先证明PB=PG，EP+PB=EG，由EG∥BC，推出$\frac{EG}{BC}$=$\frac{EQ}{QC}$=2，即可求出EG解决问题．

解答 解：如图，延长EF交BQ的延长线于G．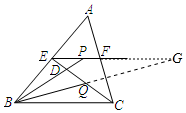

∵EG∥BC，
∴∠G=∠GBC，
∵∠GBC=∠GBP，
∴∠G=∠PBG，
∴PB=PG，
∴PE+PB=PE+PG=EG，
∵CQ=$\frac{1}{3}$EC，
∴EQ=2CQ，
∵EG∥BC，
∴$\frac{EG}{BC}$=$\frac{EQ}{QC}$=2，∵BC=4，
∴EG=8，
∴EP+PB=EG=8，
故答案为8

点评 本题考查平行线分线段成比例定理、角平分线的定义、等腰三角形的判定和性质等知识，解题的关键是学会添加辅助线构造等腰三角形解决问题，属于中考常考题型．