
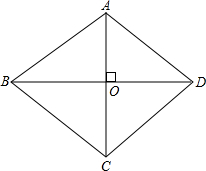
 如图,菱形的两条对角线分别是16和12,较长的一条对角线与菱形的一边的夹角为θ,tanθ=$\frac{3}{4}$.
如图,菱形的两条对角线分别是16和12,较长的一条对角线与菱形的一边的夹角为θ,tanθ=$\frac{3}{4}$. 分析 根据菱形的性质得AC⊥BD,AO=OC=$\frac{1}{2}$AC=6,BO=DO=$\frac{1}{2}$BD=8,然后在Rt△ABO中,利用正切的定义求解.
解答 解: 如图,AC=12,BD=16,∠ABD=θ,
如图,AC=12,BD=16,∠ABD=θ,
∵四边形ABCD为菱形,
∴AC⊥BD,AO=OC=$\frac{1}{2}$AC=6,BO=DO=$\frac{1}{2}$BD=8,
在Rt△ABO中,tan∠ABO=$\frac{OA}{OB}$=$\frac{6}{8}$=$\frac{3}{4}$,
即tanθ=$\frac{3}{4}$.
故答案为$\frac{3}{4}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线;菱形的面积等于对角线乘积的一半.


科目:初中数学 来源: 题型:解答题
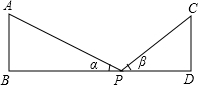 如图,在水平地面上有两座高度相同的高压电缆,铁搭AB和CD两塔底B和D之间的距离为87米,在两塔底连结BD上取一点P,测得两塔顶A和C的仰角分别为α和β,如果tanα=$\frac{3}{4}$,tanβ=$\frac{12}{13}$,求铁搭的高度.
如图,在水平地面上有两座高度相同的高压电缆,铁搭AB和CD两塔底B和D之间的距离为87米,在两塔底连结BD上取一点P,测得两塔顶A和C的仰角分别为α和β,如果tanα=$\frac{3}{4}$,tanβ=$\frac{12}{13}$,求铁搭的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
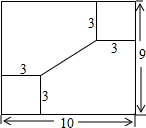 如图,工人师傅准备在一个长、宽分别是10cm,9cm的长方形铁板上打两个小孔,小孔的圆心距两边的距离都是3cm,则两孔圆心间的距离是5cm.
如图,工人师傅准备在一个长、宽分别是10cm,9cm的长方形铁板上打两个小孔,小孔的圆心距两边的距离都是3cm,则两孔圆心间的距离是5cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com