
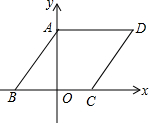
 如图,在平面直角坐标系中,?ABCD的边BC在x轴上,点A在y轴上,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
如图,在平面直角坐标系中,?ABCD的边BC在x轴上,点A在y轴上,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.分析 (1)先解一元二次方程得出OA=4,OB=3,再用勾股定理即求出AB,最后用三角函数的定义即可得出结论;
(2)分点P在OB和OC上两种情况,当点P在OB上时①分△AOP∽△OAQ和△AOP∽△QAO,用比例式建立方程求解即可;当点P在OC上时,同点P在OB上的方法即可得出结论.
解答 解:(1)由方程x2-7x+12=0解得,x=4,或x=3,
∵OA>OB,
∴OA=4,OB=3,
在Rt△AOB中,AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
∴cos∠ABC=$\frac{OB}{AB}=\frac{3}{5}$,
(2)如图,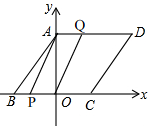 由题意得,BP=2t,AQ=6-t,
由题意得,BP=2t,AQ=6-t,
当点P在OB上时,0<t<1.5,
∵∠AOP=∠OAQ=90°,
∴①当$\frac{OP}{OA}=\frac{OA}{AQ}$时,△AOP∽△OAQ,
∴$\frac{3-2t}{3}=\frac{4}{6-t}$,
∴t=$\frac{15+\sqrt{209}}{4}$(舍)或t=$\frac{15-\sqrt{209}}{4}$,
②当$\frac{OP}{OA}=\frac{AQ}{OA}$时,△AOP∽△QAO,
∴3-2t=6-t,
∴t=-3(舍),
当点P在OC上时,1.5≤t≤3,
∵∠AOP=∠OAQ=90°,
∴①当$\frac{OP}{OA}=\frac{OA}{AQ}$,△AOP∽△OAQ,
∴$\frac{2t-3}{4}=\frac{4}{6-t}$此时方程无实数解,
②当$\frac{OP}{OA}=\frac{AQ}{OA}$,
∴2t-3=6-t,
∴t=3,
综上可得当t=$\frac{15-\sqrt{209}}{4}$或t=3时,△AOP与△QAO相似
点评 此题是相似形综合题,主要考查了一元二次方程的解法,勾股定理,锐角三角函数,相似三角形的性质等知识点;利用分类讨论的思想方法是解答本题的要点;


科目:初中数学 来源: 题型:选择题
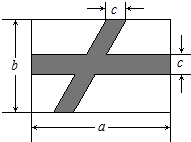 如图所示,在公园长方形空地上,要修两条路(图中的阴影所示),按照图中标的数据,计算图中空白部分的面积为( )
如图所示,在公园长方形空地上,要修两条路(图中的阴影所示),按照图中标的数据,计算图中空白部分的面积为( )| A. | ab-bc-ac+c2 | B. | bc-ab+ac | C. | b2-bc+a2-ab | D. | a2+ab+bc-ac |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
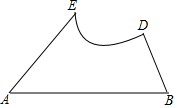 有一个三角形工件△ABC,根据安装需要,把∠C切掉了,如图,现在要在工件上画出一条线段,使它是∠C的平分线在阴影面留下的那部分.
有一个三角形工件△ABC,根据安装需要,把∠C切掉了,如图,现在要在工件上画出一条线段,使它是∠C的平分线在阴影面留下的那部分.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 数a的倒数是$\frac{1}{a}$ | B. | 数$\frac{1}{a}$的倒数是a | ||
| C. | 一个数的倒数总是比它本身大 | D. | 一个数的倒数总是比它本身小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com