
分析 首先根据题意可求得所有可能结果,然后解不等式组求得不等式组的解集得出符合要求的点的坐标,再利用概率公式即可求得答案.
解答 解:画树状图为: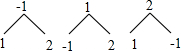
$\left\{\begin{array}{l}{\frac{3x-2}{2}<x+\frac{3}{2}①}\\{ax>b②}\end{array}\right.$,
解①得:x<5,
当a>0,
解②得:x>$\frac{b}{a}$,
根据不等式组的解集中有且只有2个非负整数解,
则2<x<5时符合要求,
故$\frac{b}{a}$=2,
即b=2,a=1符合要求,
当a<0,
解②得:x<$\frac{b}{a}$,
根据不等式组的解集中有且只有2个非负整数解,
则x<2时符合要求,
故$\frac{b}{a}$=2,
即b=-2,a=-1(舍)
故所有组合中只有1种情况符合要求,
故使关于x的不等式组的解集中有且只有2个非负整数解的概率为:$\frac{1}{6}$,
故答案为:$\frac{1}{6}$.
点评 此题考查了概率公式的应用与不等式组的解法.注意概率=所求情况数与总情况数之比,求出符合要求的点是解题关键.


科目:初中数学 来源: 题型:解答题
 如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{8}{5}$x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.
如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=-$\frac{1}{5}$x2+$\frac{8}{5}$x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABO中AB=AO=10,OB=12,以点O为原点,OB为x轴建立平面直角坐标系,点A在第一象限,直线y=x与直线AB交于点C.
如图,△ABO中AB=AO=10,OB=12,以点O为原点,OB为x轴建立平面直角坐标系,点A在第一象限,直线y=x与直线AB交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 菱形的四条变相等 | B. | 平行四边形邻边相等 | ||
| C. | 对角线相等的平行四边形是矩形 | D. | 正方形对角线相等且互相垂直平分 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形OABC的边OA、OC在坐标轴上,反比例函数$y=\frac{k}{x}$(k为常数,且k>0)的图象在第一象限与BC、AB分别交于点M、N,直线MN与y轴交于点D,若$\frac{DM}{DN}=\frac{1}{4}$,记△BMN的面积为s1,△OMN的面积为s2,则$\frac{s_1}{s_2}$的值是$\frac{3}{5}$.
如图,矩形OABC的边OA、OC在坐标轴上,反比例函数$y=\frac{k}{x}$(k为常数,且k>0)的图象在第一象限与BC、AB分别交于点M、N,直线MN与y轴交于点D,若$\frac{DM}{DN}=\frac{1}{4}$,记△BMN的面积为s1,△OMN的面积为s2,则$\frac{s_1}{s_2}$的值是$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一个几何体由若干大小相同的小立方块搭成,从上面看到的这个几何体的形状如图所示,其中小正方形中的数字表示在该位置小立方块的个数.若一个小立方块的体积为1,则这个几何体的表面积为36.
一个几何体由若干大小相同的小立方块搭成,从上面看到的这个几何体的形状如图所示,其中小正方形中的数字表示在该位置小立方块的个数.若一个小立方块的体积为1,则这个几何体的表面积为36.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com