等腰梯形一个底角是60°，它的上、下底分别是8和18，则这梯形的腰长________，高是________，面积是________．
10
分析：首先作等腰梯形的两条高，易得四边形AEFD是矩形，Rt△ABE≌Rt△DCF；根据题意两底差是10，可得BE=CF=5，又由一底角为60°，在直角三角形ABE中，可求得AB与AE；根据梯形的面积公式即可求得梯形的面积．
解答：解
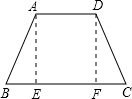
：过点A作AE⊥BC于E，过点D作DF⊥BC于F，
∴AE∥DF，∠AEB=∠DFC=90°，
∵AD∥BC，
∴四边形AEFD是矩形，
∴AD=EF，AE=DF，
∵AB=CD，
∴Rt△ABE≌Rt△DCF（HL），
∴BE=CF，
∴BE=CF=
（BC-AD）=
×（18-8）=5，
∵∠B=60°，
∴∠BAE=30°，
∴AB=10，AE=5
，
∴S
梯形ABCD=
（AD+BC）•AE=
×（18+8）×5
=65
．
点评：此题考查了等腰梯形的性质、矩形的判定与性质、全等三角形的判定与性质、直角三角形的性质等知识．解此题的关键是注意过梯形的两个顶点作梯形的两条高是解答梯形题目中的常见辅助线．
