
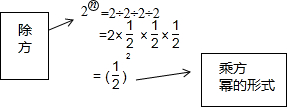 概念学习
概念学习分析 理解除方运算,利用除方运算的法则和意义解决初步探究,通过除方的法则,把深入思考的除方写成幂的形式解决(1),总结(1)得到通项(2).根据法则计算出(3)的结果.
解答 解:初步探究
(1)2③=2÷2÷2=$\frac{1}{2}$,
(-$\frac{1}{2}$)⑤=(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)=1÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)=(-2)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)=-8
故答案为:$\frac{1}{2}$,-8;
(2)A、任何非零数的圈2次方就是两个相同数相除,所以都等于1; 所以选项A正确;
B、因为多少个1相除都是1,所以对于任何正整数n,1?都等于1; 所以选项B正确;
C、3④=3÷3÷3÷3=$\frac{1}{9}$,4③=4÷4÷4=$\frac{1}{4}$,则 3④≠4③; 所以选项C错误;
D、负数的圈奇数次方,相当于奇数个负数相除,则结果是负数,负数的圈偶数次方,相当于偶数个负数相除,则结果是正数.所以选项D正确;
本题选择说法错误的,故选C;
深入思考
(1)(-3)④=(-3)÷(-3)÷(-3)÷(-3)=1×($\frac{1}{3}$)2=$\frac{1}{{3}^{2}}$;
5⑥=5÷5÷5÷5÷5÷5=1×($\frac{1}{5}$)4=$\frac{1}{{5}^{4}}$;
(-$\frac{1}{2}$)⑩=(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)÷(-$\frac{1}{2}$)
=1×2×2×2×2×2×2×2×2
=28;
故答案为:$\frac{1}{{3}^{2}}$,$\frac{1}{{5}^{4}}$,28.
(2)a?=a÷a÷a…÷a=1÷an-2=$\frac{1}{{a}^{n-2}}$.
(3):24÷23+(-8)×2③
=24÷8+(-8)×$\frac{1}{2}$
=3-4
=-1.
点评 本题考查了新运算.解决问题的关键是掌握新运算的法则,理解新运算的意义.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在正方形ABCD中,BE⊥BF,BE=BF,EF交BC于点G.
如图,在正方形ABCD中,BE⊥BF,BE=BF,EF交BC于点G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知直线y=kx与x轴的夹角为70°,P为y轴上一点,OP=6,Q为OP上一动点,M、N为直线y=kx上两动点,则PM+MQ+QN最小值为3$\sqrt{3}$.
如图,已知直线y=kx与x轴的夹角为70°,P为y轴上一点,OP=6,Q为OP上一动点,M、N为直线y=kx上两动点,则PM+MQ+QN最小值为3$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com