
【题目】把下列各式因式分解
(1)![]() (2)
(2)![]()
(3) ![]() (4)
(4)![]()
【答案】(1)(x+3)(x-3) (2)ab(a-b)2(3)![]() ;(4)
;(4)![]() .
.
【解析】
(1)运用平方差公式因式分解即可;
(2)先提取公因式ab,然后运用完全平方式因式分解即可;
(3)先运用完全平方式展开,然后合并同类项,最后运用十字相乘法因式分解即可;
(4)先运用完全平方式因式分解,然后再运用平方差公式因式分解即可.
解:(1)![]() =(x+3)(x-3);
=(x+3)(x-3);
(2)![]()
=ab(a2-2ab+b2)
=ab(a-b)2;
(3)![]()
=9(a2+2ab+b2)-4(a2-2ab+b2)
=9a2+18ab+9b2-4a2+8ab-4b2
=5a2+26ab+5b2
=(a+5b)(5a+b);
(4)![]()
=(9x2)2-2×9x2×4y2+(4y2)2
=(9x2-4y2)2
=[(3x+2y)(3x-2y)]2
=(3x+2y)2(3x-2y)2.


科目:初中数学 来源: 题型:
【题目】一辆轿车从甲城驶往乙城,同时一辆卡车从乙城驶往甲城,两车沿相同路线匀速行驶,轿车到达乙城停留一段时间后,按原路原速返回甲城;卡车到达甲城比轿车返回甲城早0.5小时,轿车比卡车每小时多行驶60千米,两车到达甲城弧均停止行驶,两车之间的路程y(千米)与轿车行驶时间t(小时)的函数图象如图所示,请结合图象提供的信息解答下列问题: 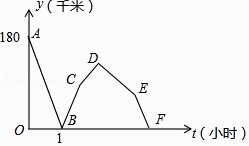
(1)请直接写出甲城和乙城之间的路程,并求出轿车和卡车的速度;
(2)求轿车在乙城停留的时间,并直接写出点D的坐标;
(3)请直接写出轿车从乙城返回甲城过程中离甲城的路程s(千米)与轿车行驶时间t(小时)之间的函数关系式(不要求写出自变量的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( ) 
A.(2,﹣3)
B.(2,3)
C.(3,2)
D.(3,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】聪聪、明明、伶伶、俐俐四人共同探究代数式![]() 的值的情况他们做了如下分工,聪聪负责找值为0时
的值的情况他们做了如下分工,聪聪负责找值为0时![]() 的值,明明负责找值为4时
的值,明明负责找值为4时![]() 的值,伶伶负责找最小值,俐俐负责找最大值,几分钟,各自通报探究的结论,其中正确的是( )
的值,伶伶负责找最小值,俐俐负责找最大值,几分钟,各自通报探究的结论,其中正确的是( )
(1)聪聪认为找不到实数![]() ,使
,使![]() 的值为0;
的值为0;
(2)明明认为只有当![]() 时,
时,![]() 的值为4;
的值为4;
(3)伶伶发现![]() 有最小值;(4)俐俐发现
有最小值;(4)俐俐发现![]() 有最大值
有最大值
A.(1)(2)B.(1)(3)C.(1)(4)D.(1)(2)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点C开始沿射线CA方向以1cm/s的速度运动;同时,点Q也从点C开始沿射线CB方向以3cm/s的速度运动.
(1)几秒后△PCQ的面积为3cm2?此时PQ的长是多少?(结果用最简二次根式表示)
(2)几秒后以A、B、P、Q为顶点的四边形的面积为22cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板ADE如图放置,连接BE,EC.下列判断:①△ABE≌△DCE;②BE=EC;③BE⊥EC;④EC=![]() DE.其中正确的有( )
DE.其中正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是 . 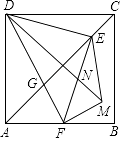
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次地震中,某村受地震影响严重,已经成为一片废墟.为重建家园,政府准备修建在地震中受损的一条公路,若由甲工程队单独修需3个月完成,每月耗资12万元;若由乙工程队单独修建需6个月完成,每月耗资5万元.
(1)请问若由甲、乙两工程队合作修建需几个月完成?共耗资多少万元?
(2)若由甲、乙两工程队先合作,剩下的由乙队来完成,且恰好历时4个月完成修建任务,求这样安排共耗资多少万元?(时间按整月计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价﹣进价),这两种服装的进价、标价如下表所示:
类型 价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)求这两种服装各购进的件数;
(2)如果A中服装按标价的8折出售,B中服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价售出少收入多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com