
【题目】甲、乙两车分别从相距480km的A.B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
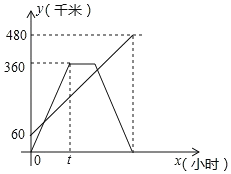
(1)乙车的速度是___千米/时,t=___小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出两车相距150千米时x的取值.
【答案】(1)60;3;(2)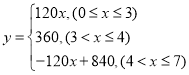 ;(3)
;(3)![]() ,
,![]() 或
或![]() 小时
小时
【解析】
(1)首先根据图示,可得乙车的速度是60千米/时,然后根据路程÷速度=时间,用两地之间的距离除以乙车的速度,求出乙车到达A地用的时间是多少;最后根据路程÷时间=速度,用两地之间的距离除以甲车往返AC两地用的时间,求出甲车的速度,再用360除以甲车的速度,求出t的值是多少即可.
(2)根据题意,分3种情况:①当0≤x≤3时;②当3<x≤4时;③4<x≤7时;分类讨论,求出甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围即可.
(3)根据题意,分3种情况:①甲乙两车相遇之前相距150千米,;②当甲车停留在C地时;③两车都朝A地行驶时,分类讨论,求出甲车出发多长时间两车相距150千米即可.
解:(1)根据图示,可得
乙车的速度是60千米/时,
甲车的速度=720÷6=120(千米/小时)
∴t=360÷120=3(小时).
故答案为:60;3;
(2)①当0≤x≤3时,设y=k1x,
把(3,360)代入,可得
3k1=360,
解得k1=120,
∴y=120x(0≤x≤3).
②当3<x≤4时,y=360.
③4<x≤7时,设y=k2x+b,
把(4,360)和(7,0)代入,可得![]() ,解得
,解得![]()
∴y=﹣120x+840(4<x≤7).
综上: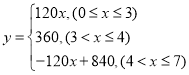
(3)①甲车朝向B地,乙车朝向A地
(480—60-150)÷(120+60)=270÷180=![]() (小时)
(小时)
②当甲车停留在C地时,
甲车刚到达C地时,两车相距:![]() (千米)
(千米)
甲车在C地停留期间:两车相距:![]() (千米),解得:
(千米),解得:![]()
③两车都朝A地行驶时,![]()
则60(![]() )+180﹣120(
)+180﹣120(![]() )=150,
)=150,
所以,![]()
解得![]()
综上,可得甲车出发![]() ,
,![]() 或
或![]() 小时后两车相距150千米.
小时后两车相距150千米.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
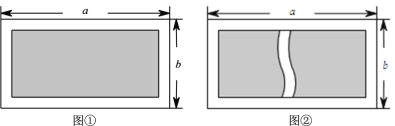
【题目】如图①,有一块长为![]() 米、宽为
米、宽为![]() 米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化.
米的长方形空地,现计划将这块空地四周均留出2米宽修道路,中间用来绿化.
(1)求绿化的面积(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
(2)若长方形空地的面积为576米2,周长为120米,求绿化的面积.
(3)若在图①的绿化部分再修一条2米宽道路,如图②,求绿化的面积(用含![]() 、
、![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用12元买软面笔记本,小丽用21元买硬面笔记本.
(1)已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗?
(2)已知每本硬面笔记本比软面笔记本贵a元,是否存在正整数a,使得每本硬面笔记本、软面笔记本的价格都是正整数,并且小明和小丽能买到相同数量的笔记本?若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB∥CD,在AB,CD内有一条折线EGF.
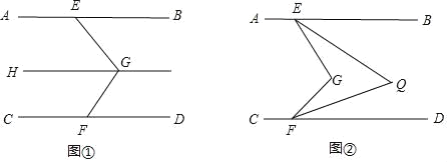
(1)如图①,过点G作GH∥AB,求证:∠BEG+∠DFG=∠EGF;
(2)如图②,已知∠BEG的平分线与∠DFG的平分线相交于点Q,请探究∠EGF与∠EQF的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商场预测某品牌运动服能够畅销,就用32000元购进了一批这种运动服,上市后很快脱销,商场又用68000元购进第二批这种运动服,所购数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该商场两次共购进这种运动服多少套?
(2)如果这两批运动服每套的售价相同,且全部售完后总利润不低于20%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
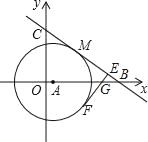
【题目】如图,在平面直角坐标系中,已知点A在x正半轴,以点A为圆心作⊙A,点M(4,4)在⊙A上,直线y=﹣![]() x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
(1)直接写出b的值和点B的坐标;
(2)求点A的坐标和圆的半径;
(3)若EF切⊙A于点F分别交AB和BC于G、E,且FE⊥BC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=![]() ,OC=
,OC=![]() ,则另一直角边BC的长为__________.
,则另一直角边BC的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适宜采用全面调查方式(普查)的是( )
A. 对襄阳市中学生每天课外读书所用时间的调查
B. 对全国中学生心理健康现状的调查
C. 对七年级(2)班学生![]() 米跑步成绩的调查
米跑步成绩的调查
D. 对市面某品牌中性笔笔芯使用寿命的调查
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com