
分析 把已知等式两边平方,利用完全平方公式化简整理求出x2+$\frac{1}{{x}^{2}}$=11,两边再平方,求出x4+$\frac{1}{{x}^{4}}$的值,原式变形后代入计算即可求出值.
解答 解:∵x-$\frac{1}{x}$=3,
∴(x-$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$-2=9,即x2+$\frac{1}{{x}^{2}}$=11,
∴x4+$\frac{1}{{x}^{4}}$=(x2+$\frac{1}{{x}^{2}}$)2-2=121-2=119,
则原式=$\frac{({x}^{8}+1)({x}^{2}+1)}{({x}^{6}+1)({x}^{4}+1)}$=$\frac{({x}^{8}+1)({x}^{2}+1)}{({x}^{2}+1)({x}^{4}-{x}^{2}+1)({x}^{4}+1)}$=$\frac{{x}^{8}+1}{({x}^{4}+1)({x}^{4}-{x}^{2}+1)}$=$\frac{{x}^{4}+\frac{1}{{x}^{4}}}{({x}^{2}+\frac{1}{{x}^{2}})({x}^{2}+\frac{1}{{x}^{2}}-1)}$=$\frac{119}{11×10}$=$\frac{119}{110}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
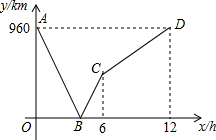 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系式.根据题中所给信息解答以下问题.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系式.根据题中所给信息解答以下问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
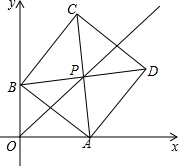 在平面直角坐标系xOy中,边长为$\sqrt{2}$的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动,顶点C、D都在第一象限.
在平面直角坐标系xOy中,边长为$\sqrt{2}$的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动,顶点C、D都在第一象限.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com