
【题目】如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD,已知BC=BD,AB=4,BC=2 ![]() .
. 
(1)求证:BD是⊙O的切线;
(2)求CD的长.
【答案】
(1)证明:∵AB为圆O的直径,
∴∠ACB=90°,
在Rt△ABC中,∵sinA= ![]() =
= ![]() =
= ![]() ,
,
∴∠A=60°,
∵AO=CO,
∴△AOC为等边三角形,
∴∠AOC=∠ACO=60°,
∴∠BCD=∠ACB﹣∠ACO=90°﹣60°=30°,
∵∠BOD=∠AOC=60°,
∴∠OBD=180°﹣(∠BOD+∠D)=90°,
∴OB⊥BD,
则BD为圆O的切线
(2)解:∵AB为圆O的直径,且AB=4,
∴OB=OC=2,
∵BC=BD,
∴∠BCD=∠D,
∵OC=OB,
∴∠BCD=∠OBC,
∴∠D=∠OBC,
在△BCD和△OCB中,
∠D=∠OBC,∠BCD=∠OCB,
∴△BCD∽△OCB,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
则CD=6
【解析】(1)由AB为圆的直径,利用直径所对的圆周角为直角得到∠ACB为直角,进而得到三角形ABC为直角三角形,利用锐角三角函数定义求出sinA的值,利用特殊角的三角函数值求出∠A的度数为60度,再由OA=OC,得到三角形AOC为等边三角形,利用等边三角形的性质得到两个角为60度,进而求出∠BCD为30度,利用三角形内角和定理求出∠OBD为直角,即OB垂直于BD,即可得证;(2)由AB为直径,求出半径为2,由BC=BD,利用等边对等角得到一对角相等,再由OC=OB得到一对角相等,等量代换得到∠D=∠OBC,再由一对公共角相等,得到三角形OCB与三角形BCD相似,由相似得比例,即可求出CD的长.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】小赵和小王交流暑假中的活动,小赵说:“我们一家外出旅行了一个星期,这7天的日期数之和是84天,你知道我们几号出去的么?”小王说“我暑假去舅舅家住了7天,日历数再加月份数也是84,你能猜出我是几月几号回的家?试试看列出方程,解决小赵、小王的问题.(提示:7月1日﹣9月1日暑假) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米.
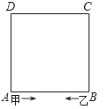
(1)出发后 分钟时,甲乙两人第一次在正方形的顶点处相遇;
(2)如果用记号(a,b)表示两人行了a分钟,并相遇过b次,那么当两人出发后第一次处在正方形的两个相对顶点位置时,对应的记号应是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xoy中,点A、B的坐标分别是A(-1,0),B(3,0),将线段AB向上平移2个单位,再向右平移1个单位,得到线段DC,点A、B的对应点分别是D、C,连接AD、BC.
(1)直接写出点C,D的坐标;
(2)求四边形ABCD的面积;
(3)点P为线段BC上任意一点(与点B、C不重合),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.

查看答案和解析>>
科目:初中数学 来源: 题型:
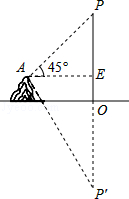
【题目】在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式: ![]() =
= ![]() )( )
)( )
A.25 ![]() +75
+75
B.50 ![]() +50
+50
C.75 ![]() +75
+75
D.50 ![]() +100
+100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x1、x2是一元二次方程2x2﹣7x+5=0的两根,利用一元二次方程根与系数的关系,求下列各式的值.
(1)x12x2+x1x22; (2)(x1﹣x2)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.
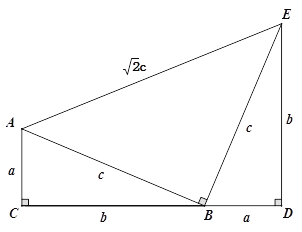
请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.
等级 | 人数/名 |
优秀 | a |
良好 | b |
及格 | 150 |
不及格 | 50 |
解答下列问题:
(1)a等于多少?,b等于多少?
(2)补全条形统计图;
(3)试估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=80°,求∠BOD的度数;
(2)若∠EOC=∠EOD,求∠BOD的度数.
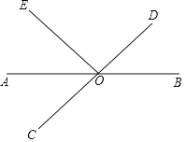
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com