
ЁОЬтФПЁПШчЭМ1ЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃЌDЮЊBCБпЩЯвЛЕу(ВЛгыЕуBЃЌCжиКЯ)ЃЌНЋЯпЖЮADШЦЕуAФцЪБеыа§зЊ90ЁуЕУЕНAEЃЌСЌНгEC.
(1)ШчЭМ1ЃЌЭЈЙ§ЭМаЮа§зЊЕФаджЪПЩжЊADЃН_____ЃЌЁЯDAEЃН_____ЖШ.
ЃЈНтОіЮЪЬтЃЉ
(2)ШчЭМ1ЃЌжЄУїBCЃНDC+ECЃЛ
ЃЈЭиеЙбгЩьЃЉ
ШчЭМ2ЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃЌDЮЊЁїABCЭтвЛЕуЃЌЧвЁЯADCЃН45ЁуЃЌШдНЋЯпЖЮADШЦЕуAФцЪБеыа§зЊ90ЁуЕУЕНAEЃЌСЌНгECЃЌED.
(3)ШєADЃН6ЃЌCDЃН3ЃЌЧѓBDЕФГЄ.
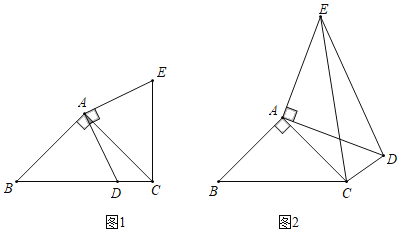
ЁОД№АИЁП(1)AEЃЌ90ЃЛ(2)жЄУїМћНтЮіЃЛ(3)BD=9.
ЁОНтЮіЁП
(1)РћгУа§зЊБфЛЛЕФаджЪМДПЩНтОіЮЪЬтЃЛ(2)жЄУїЁїABDЁеЁїACE(SAS)ЃЌЭЦГіBDЃНCEЃЌПЩЕУНсТлЃЛ(3)ШчЭМ2жаЃЌСЌBD.жЄУїЁїABDЁеЁїACE(SAS)ЃЌЭЦГіBDЃНCEЃЌдйжЄУїЁїECDЪЧжБНЧШ§НЧаЮЃЌРћгУЙДЙЩЖЈРэМДПЩНтОіЮЪЬт.
НтЃК
(1)гЩа§зЊЕФаджЪПЩжЊЃКADЃНAEЃЌЁЯDAEЃН90Ёу.
ЙЪД№АИЮЊAEЃЌ90.
(2)ШчЭМ1жаЃЌ
ЁпЁЯDAEЃНЁЯBACЃЌ
ЁрЁЯBADЃНЁЯCAEЃЌ
гжЁпABЃНACЃЌADЃНAEЃЌ
ЁрЁїABDЁеЁїACE(SAS)ЃЌ
ЁрBDЃНCEЃЌ
ЁрBCЃНBD+DCЃНEC+CD.
(3)ШчЭМ2жаЃЌСЌBD.
ЁпЁЯBACЃНЁЯDAEЃЌ
ЁрBADЃНЁЯCAEЃЌ
гжЁпABЃНACЃЌADЃНAEЃЌ
ЁрЁїABDЁеЁїACE(SAS)ЃЌ
ЁрBDЃНCEЃЌ
ЖјЁЯADEЃНЁЯADCЃН45ЁуЃЌ
ЁрЁїECDЮЊжБНЧШ§НЧаЮЃЌ
ЁрEC2ЃНCD2+ED2ЃНCD2+2AD2ЃН81ЃЌ
ЁрECЃН9ЃЌМДЃКBDЕФГЄЮЊ9.


 НЬВФШЋНтзжДЪОфЦЊЯЕСаД№АИ
НЬВФШЋНтзжДЪОфЦЊЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§yЃНx2Љ4ЕФЭМЯѓгыxжсНЛгкЕуAЁЂBЃЈЕуAЮЛгкЕуBЕФзѓВрЃЉЃЌCЮЊЖЅЕуЃЎвЛДЮКЏЪ§yЃНmx+2ЕФЭМЯѓОЙ§ЕуAЃЌгыyжсНЛгкЕуDЃЎ
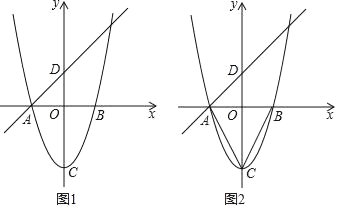
ЃЈ1ЃЉЧѓжБЯпADЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЦНвЦИУХзЮяЯпЕУЕНвЛЬѕаТХзЮяЯпЃЌЩшаТХзЮяЯпЕФЖЅЕуЮЊCЁфЃЎШєаТХзЮяЯпЕФЖЅЕуКЭдХзЮяЯпЕФЖЅЕуЕФСЌЯпCCЁфЦНаагкжБЯпADЃЌЧвЕБ1ЁмxЁм3ЪБЃЌаТХзЮяЯпЖдгІЕФКЏЪ§жЕгазюаЁжЕЮЊЉ1ЃЌЧѓаТХзЮяЯпЖдгІЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉШчЭМЃЌСЌНгACЁЂBCЃЌдкзјБъЦНУцФкЃЌжБНгаДГіЪЙЕУЁїACDгыЁїEBCЯрЫЦЃЈЦфжаЕуAгыЕуEЪЧЖдгІЕуЃЉЕФЕуEЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЯњЪлЕФФГжжЩЬЦЗУПМўЕФБъМлЪЧ![]() дЊЃЌШєАДБъМлЕФАЫелЯњЪлЃЌШдПЩгЏРћ
дЊЃЌШєАДБъМлЕФАЫелЯњЪлЃЌШдПЩгЏРћ![]() ЃЌДЫЪБИУжжЩЬЦЗУПаЧЦкПЩТєГі
ЃЌДЫЪБИУжжЩЬЦЗУПаЧЦкПЩТєГі![]() МўЃЌЪаГЁЕїВщЗЂЯжЃКдкАЫелЯњЪлЕФЛљДЁЩЯЃЌИУжжЩЬЦЗУПНЕМл
МўЃЌЪаГЁЕїВщЗЂЯжЃКдкАЫелЯњЪлЕФЛљДЁЩЯЃЌИУжжЩЬЦЗУПНЕМл![]() дЊЃЌУПаЧЦкПЩЖрТє
дЊЃЌУПаЧЦкПЩЖрТє![]() МўЃЎЩшУПМўЩЬЦЗНЕМл
МўЃЎЩшУПМўЩЬЦЗНЕМл![]() дЊЃЈ
дЊЃЈ![]() ЮЊећЪ§ЃЉЃЌУПаЧЦкЕФРћШѓЮЊ
ЮЊећЪ§ЃЉЃЌУПаЧЦкЕФРћШѓЮЊ![]() дЊ
дЊ
ЃЈ1ЃЉЧѓИУжжЩЬЦЗУПМўЕФНјМлЮЊЖрЩйдЊЃП
ЃЈ2ЃЉЕБЪлМлЮЊЖрЩйЪБЃЌУПаЧЦкЕФРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉ2019Фъ2дТИУжжЩЬЦЗУПаЧЦкЕФЪлМлОљЮЊУПМў![]() дЊЃЌШє2019Фъ2дТЕФРћШѓВЛЕЭгк
дЊЃЌШє2019Фъ2дТЕФРћШѓВЛЕЭгк![]() дЊЃЌЧыЧѓГі
дЊЃЌЧыЧѓГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпC1ЃКyЃНaЃЈx+2ЃЉ2Љ5ЕФЖЅЕуЮЊPЃЌгыxжсЯрНЯгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌЧвЕуBЕФзјБъЮЊЃЈ1ЃЌ0ЃЉ
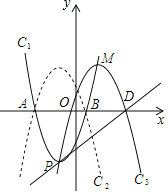
ЃЈ1ЃЉЧѓХзЮяЯпC1ЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЃЌХзЮяЯпC2гыХзЮяЯпC1ЙигкxжсЖдГЦЃЌНЋХзЮяЯпC2ЯђгвЦНвЦЃЌЦНвЦКѓЕФХзЮяЯпМЧЮЊC3ЃЌХзЮяЯпC3ЕФЖЅЕуЮЊMЃЌЕБЕуPЃЌMЙигкЕуOГЩжааФЖдГЦЪБЃЎЂйЧѓЕуMЕФзјБъЃЛЂкЧѓХзЮяЯпC3ЕФНтЮіЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЩшХзЮяЯпC3гыxжсЕФе§АыжсНЛгкЕуDЃЌдкжБЯпPDЕФЩЯЗНЕФХзЮяЯпC3ЩЯЃЌЪЧЗёДцдкЕуQЪЙЕУЁїPDQЕФУцЛ§зюДѓЃПШєДцдкЃЌЧѓГіЕБЕуQЕФКсзјБъЮЊКЮжЕЪБЁїPDQУцЛ§зюДѓЃЌШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧХзЮяЯпаЭЙАЧХЃЌЕБЙАЖЅРыЫЎУц2mЪБЃЌЫЎУцПэ4mЃЌЫЎУцЯТНЕ2mЃЌЫЎУцПэЖШдіМг______m.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЕФШ§ИіЖЅЕуЗжБ№ЮЊ
ЕФШ§ИіЖЅЕуЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
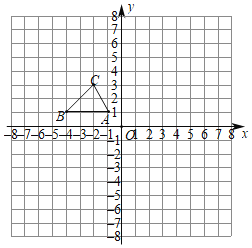
ЃЈ1ЃЉЛГі![]() ЙигкЕуOГЩжааФЖдГЦЕФ
ЙигкЕуOГЩжааФЖдГЦЕФ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉвдЕуAЮЊЮЛЫЦжааФЃЌНЋ![]() ЗХДѓЮЊдРДЕФ2БЖЃЌЕУЕН
ЗХДѓЮЊдРДЕФ2БЖЃЌЕУЕН![]() ЃЌЧыдкЕкЖўЯѓЯоФкЛГі
ЃЌЧыдкЕкЖўЯѓЯоФкЛГі![]() ЃЛ
ЃЛ
ЃЈ3ЃЉжБНгаДГівдЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖЅЕуЃЌвд
ЮЊЖЅЕуЃЌвд![]() ЮЊвЛБпЕФЦНааЫФБпаЮЕФЕкЫФИіЖЅЕуDЕФзјБъЃЎ
ЮЊвЛБпЕФЦНааЫФБпаЮЕФЕкЫФИіЖЅЕуDЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
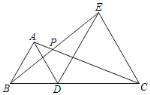
ЁОЬтФПЁПШчЭМЃЌBCЃН8![]() cmЃЌЕуDЪЧЯпЖЮBCЩЯЕФвЛЕуЃЌЗжБ№вдBDЁЂCDЮЊБпдкBCЕФЭЌВрзїЕШБпШ§НЧаЮABDКЭЕШБпШ§НЧаЮCDEЃЌACЁЂBEЯрНЛгкЕуPЃЌдђЕуDДгЕуBдЫЖЏЕНЕуCЪБЃЌЕуPЕФдЫЖЏТЗОЖГЄЃЈКЌгыЕуBЁЂCжиКЯЃЉЮЊ_____ЃЎ
cmЃЌЕуDЪЧЯпЖЮBCЩЯЕФвЛЕуЃЌЗжБ№вдBDЁЂCDЮЊБпдкBCЕФЭЌВрзїЕШБпШ§НЧаЮABDКЭЕШБпШ§НЧаЮCDEЃЌACЁЂBEЯрНЛгкЕуPЃЌдђЕуDДгЕуBдЫЖЏЕНЕуCЪБЃЌЕуPЕФдЫЖЏТЗОЖГЄЃЈКЌгыЕуBЁЂCжиКЯЃЉЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєКЏЪ§![]() ЪЧ
ЪЧ![]() Йигк
Йигк![]() ЕФЗДБШР§КЏЪ§ЁЃ
ЕФЗДБШР§КЏЪ§ЁЃ
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉКЏЪ§ЭМЯѓдкФФаЉЯѓЯоЃПдкУПИіЯѓЯоФкЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјдѕбљБфЛЏЃП
ЕФдіДѓЖјдѕбљБфЛЏЃП
ЃЈ3ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЁЃ
ЕФШЁжЕЗЖЮЇЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
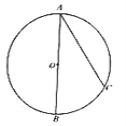
ЁОЬтФПЁПЃЈБОЬт9ЗжЃЉШчЭМЃЌ![]() ЪЧ
ЪЧ![]() ЕФжБОЖЃЌ
ЕФжБОЖЃЌ![]() ЪЧ
ЪЧ![]() ЩЯвЛЕуЃЌСЌНг
ЩЯвЛЕуЃЌСЌНг![]() .Й§Еу
.Й§Еу![]() зї
зї![]() ЕФЧаЯпЃЌНЛ
ЕФЧаЯпЃЌНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌдк
ЃЌдк![]() ЩЯШЁвЛЕу
ЩЯШЁвЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() .ЧыВЙШЋЭМаЮВЂНтОіЯТУцЕФЮЪЬтЃК
.ЧыВЙШЋЭМаЮВЂНтОіЯТУцЕФЮЪЬтЃК
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЙћ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com