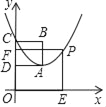
[题目]如图.在平面直角坐标系中.点AB坐标分别为(1.1).(1.2).经过A.B作y轴的垂线分别交于D.C两点.得到正方形ABCD.抛物线y=x2+bx+c经过A.C两点.点P为第一象限内抛物线上一点(不与点A重合).过点P分别作PF∥x轴交y轴于点F.PE∥y轴交x轴于点E.设点P的横坐标为m.矩形PFOE与正方形ABCD重叠部分图形的周长为L．(1)求抛物线的解析式．( 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，在平面直角坐标系中，点AB坐标分别为（1，1）、（1，2），经过A、B作y轴的垂线分别交于D、C两点，得到正方形ABCD，抛物线y=x2+bx+c经过A、C两点，点P为第一象限内抛物线上一点（不与点A重合），过点P分别作PF∥x轴交y轴于点F，PE∥y轴交x轴于点E，设点P的横坐标为m，矩形PFOE与正方形ABCD重叠部分图形的周长为L．

（1）求抛物线的解析式．

（2）当矩形PFOE的面积被抛物线的对称轴平分时，求m的值．

（3）当m＜2时，求L与m之间的函数关系式．

（4）设线段BD与矩形PFOE的边交于点Q，当△FDQ为等腰直角三角形时，直接写出m的取值范围．

【答案】（1）：y=x2﹣2x+2；（2）m=2；（3）当0＜m＜1时，L=2m2﹣2m+2；当1＜m＜2时，L=2m2﹣4m+4；（4）当△FDQ为等腰直角三角形时，m的取值范围为≤m＜1和1＜m≤2或m=2﹣

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】问题情境

小明和小丽共同探究一道数学题：

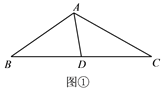
如图①，在△ABC中，点D是边BC的中点，∠BAD=65°，∠DAC=50°，AD=2，

求AC．

探索发现

小明的思路是：延长AD至点E，使DE=AD，构造全等三角形．

小丽的思路是：过点C作CE∥AB，交AD的延长线于点E，构造全等三角形．

选择小明、小丽其中一人的方法解决问题情境中的问题．

类比应用

如图②，在四边形ABCD中，对角线AC、BD相交于点O，点O是BD的中点，

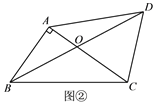
AB⊥AC．若∠CAD=45°，∠ADC=67.5°，AO=2，则BC的长为___________．

查看答案和解析>>

科目：初中数学 来源： 题型：

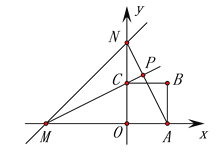
【题目】如图直线y=x+2分别与x轴，y轴交于点M、N，边长为1的正方形OABC的一个顶点O在坐标系原点，直线AN与MC交于点P，若正方形绕点O旋转一周，则点P到点（0,1）长度的最小值是___________.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】点（a，y1）（a+2，y2）都在反比例函数y＝（k＜0）的图象上，若y1＞y2，则a的取值范围是_____．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】近年来，我国很多地区持续出现雾霾天气．某社区为了调查本社区居民对雾霾天气主要成因的认识情况，随机对该社区部分居民进行了问卷调查，要求居民从五个主要成因中只选择其中的一项，被调查居民都按要求填写了问卷．社区对调查结果进行了整理，绘制了如下不完整的统计图表．被调查居民选择各选项人数统计表

雾霾天气的主要成因	频数（人数）
A大气气压低，空气不流动	m
B地面灰尘大，空气湿度低	40
C汽车尾气排放	n
D工厂造成的污染	120
E其他	60