
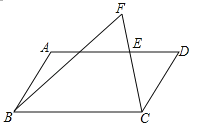
【题目】如图,在ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE.
(1)求证:∠D=∠F;
(2)用直尺和圆规在AD上作出一点P,使△BPC∽△CDP(保留作图的痕迹,不写作法).
【答案】(1)证明见解析;(2)答案见解析.
【解析】
(1)BE交AD于G,先利用AD∥BC得到∠FBC=∠FGE,加上∠FBC=∠DCE,所以∠FGE=∠DCE,然后根据三角形内角和定理易得∠D=∠F;
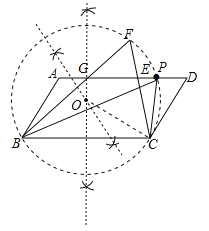
(2)分别作BC和BF的垂直平分线,它们相交于点O,然后以O为圆心,OC为半径作△BCF的外接圆⊙O,⊙O交AD于P,连结BP、CP,则根据圆周角定理得到∠F=∠BPC,而∠F=∠D,所以∠D=∠BPC,接着可证明∠PCD=∠APB=∠PBC,于是可判断△BPC∽△CDP.
解:(1)BE交AD于G.如图,∵四边形ABCD为平行四边形,∴AD∥BC,∴∠FBC=∠FGE.
而∠FBC=∠DCE,∴∠FGE=∠DCE.
∵∠GEF=∠DEC,∴∠D=∠F;
(2)如图,点P为所作.


科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按![]() 元销售时,每天可销售
元销售时,每天可销售![]() 个;若销售单价每降低元,每天可多售出
个;若销售单价每降低元,每天可多售出![]() 个.已知每个玩具的固定成本为
个.已知每个玩具的固定成本为![]() 元,问这种玩具的销售单价为多少元时,厂家每天可获利润
元,问这种玩具的销售单价为多少元时,厂家每天可获利润![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
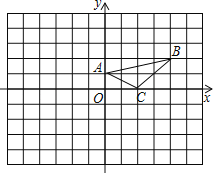
【题目】如图,在平面直角坐标系中,A(0,1),B(4,2),C(2,0).
(1)将△ABC沿y轴翻折得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕着点(﹣1,﹣1)旋转180°得到△A2B2C2,画出△A2B2C2;
(3)线段B2C2可以看成是线段B1C1绕着平面直角坐标系中某一点逆时针旋转得到,直接写出旋转中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(1)第1个等式:a1=![]() ; 第2个等式:a2=
; 第2个等式:a2=![]() ;
;
第3个等式:a3=![]() ; 第4个等式:a4=
; 第4个等式:a4=![]() ;
;
…
用含有n的代数式表示第n个等式:an=___________=___________(n为正整数);
(2)按一定规律排列的一列数依次为![]() ,1,
,1, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…,按此规律,这列数中的第100个数是_______________.
,…,按此规律,这列数中的第100个数是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图
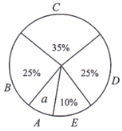
根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扬州某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,若乙团队人数不超过40人,甲团队人数不超过80人,设甲团队人数为![]() 人,如果甲、乙两团队分别购买门票,两团队门票款之和为
人,如果甲、乙两团队分别购买门票,两团队门票款之和为![]() 元.
元.

(1)直接写出![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)计算甲、乙两团队联合购票比分别购票最多可节约多少钱?
(3)该景区每年11月、12月为淡季,景区决定在这两个月实行门票打五折的优惠(打折期间不售团体票),以吸引大量游客,提高景区收入;景区经过调研发现,随着接待游客数的增加,景区的运营成本也随之增加,景区运营成本![]() (万元)与两个月游客总人数
(万元)与两个月游客总人数![]() (万人)之间满足函数关系式:
(万人)之间满足函数关系式:![]() ;两个月游客总人数
;两个月游客总人数![]() (万人)满足:
(万人)满足:![]() ,且淡季每天游客数基本相同;为了获得最大利润,景区决定通过网络预约购票的方式控制淡季每天游客数,请问景区的决定是否正确?并说明理由.(利润
,且淡季每天游客数基本相同;为了获得最大利润,景区决定通过网络预约购票的方式控制淡季每天游客数,请问景区的决定是否正确?并说明理由.(利润![]() 门票收入
门票收入![]() 景区运营成本)
景区运营成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两把不同的锁和四把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁.现在任意取出一把钥匙去开任意一把锁.
(1)请用列表或画树状图的方法表示出上述试验所有可能结果;
(2)求一次打开锁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从如图所示的二次函数![]() 的图象中,观察得出了下面五条信息:①c>0,②abc<0,③a-b+c>0,④
的图象中,观察得出了下面五条信息:①c>0,②abc<0,③a-b+c>0,④![]() >4ac,⑤2a=-2b,其中正确结论是( ).
>4ac,⑤2a=-2b,其中正确结论是( ).
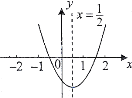
A.①②④B.②③④C.③④⑤D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:两个相似等腰三角形,如果它们的底角有一个公共的顶点,那么把这两个三角形称为“关联等腰三角形”.如图,在![]() 与
与![]() 中,
中,![]() ,且
,且![]() 所以称
所以称![]() 与
与![]() 为“关联等腰三角形”,设它们的顶角为
为“关联等腰三角形”,设它们的顶角为![]() ,连接
,连接![]() ,则称
,则称![]() 会为“关联比".
会为“关联比".
下面是小颖探究“关联比”与α之间的关系的思维过程,请阅读后,解答下列问题:
[特例感知]
![]() 当
当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,
时,
①在图1中,若点![]() 落在
落在![]() 上,则“关联比”
上,则“关联比”![]() =
=
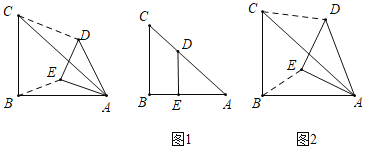
②在图2中,探究![]() 与
与![]() 的关系,并求出“关联比”
的关系,并求出“关联比”![]() 的值.
的值.

[类比探究]
![]() 如图3,
如图3,
①当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,“关联比”
时,“关联比”![]() =
=
②猜想:当![]() 与
与![]() 为“关联等腰三角形”,且
为“关联等腰三角形”,且![]() 时,“关联比”
时,“关联比”![]() = (直接写出结果,用含
= (直接写出结果,用含![]() 的式子表示)
的式子表示)
[迁移运用]
![]() 如图4,
如图4, ![]() 与
与![]() 为“关联等腰三角形”.若
为“关联等腰三角形”.若![]() 点
点![]() 为
为![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 为
为![]() 上一动点,求点
上一动点,求点![]() 自点
自点![]() 运动至点
运动至点![]() 时,点
时,点![]() 所经过的路径长.
所经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com