
分析 (1)等量关系为:(40-30+涨价的价格)×(原来卖出的数量-10×涨价的价格)=8000,把相关数值代入求合适的解即可;
(2)设最大利润为y元,根据(1)列出y与x的二次函数关系式,转化为顶点式解决最值.
解答 (1)解:设售价定为x元时,每天赚取利润8000元,
由已知得:(x-30)[500-10(x-40)]=8000,
整理得:x2-120x+3500=0,
解得:x1=50或x2=70
∵尽量减少库存,
∴x=50,
答:售价定为50元时,每天赚取利润8000元.
(2)解:设最大利润为y元,由题可得:y=(x-30)[500-10(x-40)]
$\begin{array}{l}=-10{x^2}+1200x-27000\\=-10{({x-60})^2}+9000\end{array}$
当x=60时,ymax=9000,
答:当售价定为60元时,有最大利润,最大利润为11000元.
点评 本题考查一元二次方程的应用以及运用二次函数与一元二次方程的关系解决最值问题,得到每件商品获得的利润和卖出商品件数是解决本题的突破点,构建二次函数模型是解决最大利润问题的关键.


科目:初中数学 来源: 题型:解答题
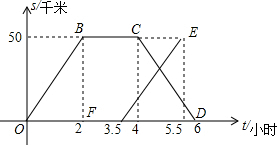 为搜集植物标本,老师带领第一组同学从学校先乘车出发,寻找到目的地,采集中,向另一组同学报告,采完后立即返回,第二组同学接到报告后,立即从学校出发,如图是两组同学与学校的距离s和离开学校的时间t之间的函数图象.(假设两组同学沿同一路线行进)
为搜集植物标本,老师带领第一组同学从学校先乘车出发,寻找到目的地,采集中,向另一组同学报告,采完后立即返回,第二组同学接到报告后,立即从学校出发,如图是两组同学与学校的距离s和离开学校的时间t之间的函数图象.(假设两组同学沿同一路线行进)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
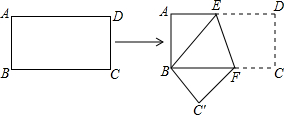
 如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.若CG=8,则S四边形BCDG=16$\sqrt{3}$.
如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.若CG=8,则S四边形BCDG=16$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图小明在楼上点A处测得旗杆BC顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面高AD为12m,旗杆的高度为16 m.
如图小明在楼上点A处测得旗杆BC顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面高AD为12m,旗杆的高度为16 m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$ | B. | $\sqrt{{x}^{2}+1}$ | C. | $\sqrt{{y}^{3}}$ | D. | $\sqrt{\frac{1}{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<11 | B. | m>11 | C. | m≤11 | D. | m≥11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com