
| 成绩/分 | 56 | 57 | 58 | 59 | 60 |
| 人数 | 1 | 2 | 1 | 2 | 4 |
| A. | 这10名学生体育成绩的中位数为58 | B. | 这10名学生体育成绩的平均数为58 | ||
| C. | 这10名学生体育成绩的众数为60 | D. | 这10名学生体育成绩的方差为60 |
分析 根据中位数的定义对A进行判断;根据平均数的计算公式对B进行判断;根据众数的定义对C进行判断;利用方差公式对D进行判断.
解答 解:这10名学生体育成绩的中位数为$\frac{59+59}{2}$=59,这10名学生体育成绩的众数为60,这10名学生体育成绩的平均数=$\frac{1}{10}$(56+57×2+58+59×2+60×4)=58.6,
这10名学生体育成绩的方差=$\frac{1}{10}$[(56-58.6)2+2×(57-58.6)2+(58-58.6)2+2×(59-58.6)2+4×(60-58.6)2]=15.4.
故选C.
点评 本题考查了方差:方差的计算公式是:s2=$\frac{1}{n}$[(x1-x?)2+(x2-x?)2+…+(xn-x?)2](可简单记忆为“方差等于差方的平均数”);方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.也考查了平均数、中位数和众数.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 900元 | B. | 920元 | C. | 960元 | D. | 980元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
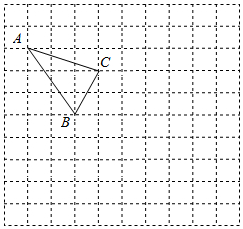 如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点)ABC的顶点A,C的坐标分别为(-4,4),(-1,3).
如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点)ABC的顶点A,C的坐标分别为(-4,4),(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
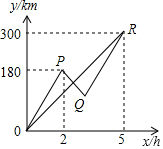 已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发x小时后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.
已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发x小时后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.4×108 | B. | 0.34×109 | C. | 3.38×108 | D. | 3.39×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在点D′,C′的位置,若∠EFB=70°,则∠AED′等于( )
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在点D′,C′的位置,若∠EFB=70°,则∠AED′等于( )| A. | 40° | B. | 50° | C. | 65° | D. | 70° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com