Question

17．如图，在平面直角坐标系中，已知A（a，0），B（b，0），其中a，b满足|a+1|+（b-3）²=0．
（1）填空：a=-1，b=3；
（2）如果在第三象限内有一点M（-2，m），请用含m的式子表示△ABM的面积；
（3）在（2）条件下，当m=-$\frac{3}{2}$时，在y轴上有一点P，使得△BMP的面积与△ABM的面积相等，请求出点P的坐标．

Answer 1

分析 （1）根据非负数性质可得a、b的值；
（2）根据三角形面积公式列式整理即可；
（3）先根据（2）计算S_△ABM，再分两种情况：当点P在y轴正半轴上时、当点P在y轴负半轴上时，利用割补法表示出S_△BMP，根据S_△BMP=S_△ABM列方程求解可得．

解答 解：（1）∵|a+1|+（b-3）²=0，
∴a+1=0且b-3=0，
解得：a=-1，b=3，
故答案为：-1，3；

（2）过点M作MN⊥x轴于点N，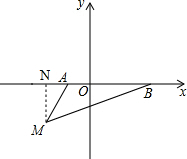

∵A（-1，0）B（3，0）
∴AB=1+3=4，
又∵点M（-2，m）在第三象限
∴MN=|m|=-m
∴S_△ABM=$\frac{1}{2}$AB•MN=$\frac{1}{2}$×4×（-m）=-2m；

（3）当m=-$\frac{3}{2}$时，M（-2，-$\frac{3}{2}$）
∴S_△ABM=-2×（-$\frac{3}{2}$）=3，
点P有两种情况：①当点P在y轴正半轴上时，设点p（0，k）
   
S_△BMP=5×（$\frac{3}{2}$+k）-$\frac{1}{2}$×2×（$\frac{3}{2}$+k）-$\frac{1}{2}$×5×$\frac{3}{2}$-$\frac{1}{2}$×3×k=$\frac{5}{2}$k+$\frac{9}{4}$，
∵S_△BMP=S_△ABM，
∴$\frac{5}{2}$k+$\frac{9}{4}$=3，
解得：k=0.3，
∴点P坐标为（0，0.3）；
②当点P在y轴负半轴上时，设点p（0，n），

S_△BMP=-5n-$\frac{1}{2}$×2×（-n-$\frac{3}{2}$）-$\frac{1}{2}$×5×$\frac{3}{2}$-$\frac{1}{2}$×3×（-n）=-$\frac{5}{2}$n-$\frac{9}{4}$，
∵S_△BMP=S_△ABM，
∴-$\frac{5}{2}$n-$\frac{9}{4}$=3，
解得：n=-2.1
∴点P坐标为（0，-2.1），
故点P的坐标为（0，0.3）或（0，-2.1）．

点评 本题主要考查坐标与图形的性质，利用割补法表示出△BMP的面积，并根据题意建立方程是解题的关键．