
����Ŀ��ij�̼�����һ����Ʒ������һ��ʱ����֣�ÿ�������y�������뵱������۵���x��Ԫ/��������һ�κ�����ϵ�����ҵ�x��30ʱ��y��500����x��35ʱ��y��450����۲��Ź涨������Ʒ�����۵��۲��ܳ���48Ԫ/����������Ʒ�Ķ���Ϊ30Ԫ��ʵ�ʰ����۵�8�۳��ۣ���Ȼ���Ի��20%������
��1�������Ʒ�ijɱ��ۺ�ÿ���õ��������
��2���ù�˾ÿ����Ҫ�˹���ˮ��ͷ���֧������bԪ����������һ���غ�˾���������Ҫ������8000Ԫ��8500Ԫ֮�䣨����8000��8500�������b��ȡֵ��Χ��
��3��������Ʒ�Ľ��۸�ΪaԪ��ÿ��������뵱������۵��۵Ĺ�ϵ���䣬��30��x��48ʱ������Ʒ������x�������������a��ȡֵ��Χ��
���𰸡���1������Ʒ�ijɱ���Ϊ20Ԫ��ÿ���õ��������Ϊ8960Ԫ����2��500��b��1000����3��0��a��16��
��������
(1)��������=���������ɱ���������=������������������ʽ���㼴�ɣ�
(2)����(1)����������b��������8000Ԫ��8500Ԫ֮�䣬�������b��ȡֵ��Χ��
(3)���ݶ��κ��������ʵ�30��x��48ʱ�����ڶԳ�����࣬����Ʒ������x�������������ȷ��a��ȡֵ��Χ��
(1)��ÿ�������y(��)�뵱������۵���x(Ԫ/��)�����һ�κ�����ϵʽΪ��
y=kx+b��
��x=30ʱ��y=500����x=35ʱ��y=450����ã�
k=��10��b=800��
��һ�κ�����ϵʽΪ��y=��10x+800��
�����Ʒ�ijɱ���ΪaԪ���������⣬�ã�
![]()
��ã�a=20��
��ÿ���õ�����ΪwԪ���������⣬��
![]()
![]()
�ߩ�10��0�����۵��۲��ܳ���48Ԫ/����
��x��48ʱ��w��x�����������
�൱x=48ʱ��w�����ֵ�����ֵΪ8960��
�𣺸���Ʒ�ijɱ���Ϊ20Ԫ��ÿ���õ��������Ϊ8960Ԫ��
(2)�߸ù�˾ÿ����Ҫ�˹���ˮ��ͷ���֧������bԪ��
�������Ҫ������8000Ԫ��8500Ԫ֮�䣬
��8000��9000��b��8500
��500��b��1000��
(3)�������⣬��
w=(x��a)(��10x+800)
=��10x2+(800+10a)x��800a
�ߵ�30��x��48ʱ������Ʒ������x�����������
�Գ���![]()
��![]() ��48
��48
��ã�a��16
��a��ȡֵ��Χ�ǣ�0��a��16��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��ͼ����
��ͼ����![]() (1��0).
(1��0).
(1)��![]() ,
,![]() ʱ������κ����Ľ���ʽ�����κ�����Сֵ��
ʱ������κ����Ľ���ʽ�����κ�����Сֵ��
(2)���κ�����ͼ����![]() (
(![]() ,
,![]() )��
)��![]() (
(![]() ��
��![]() ).��������ʵ��
).��������ʵ��![]() ������ֵ
������ֵ![]() ����С��
����С��![]() �����ʱ���κ����Ľ���ʽ.
�����ʱ���κ����Ľ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ȡ������̫ƽ��֮����������ǻ���������Ҫ�����֮һ.ij����й����������ĸ�ƽ�����ݽ��.С����С�������һ���ݽ�����������ͨ������Ϸ������˭��һ������.����Ϸ�����ǣ���һ�������Ĵ�������һ������a����������b��c��(����ɫ����������ͬ)��С���Ӵ���������һ���Żغ���ȣ�С���ٴӴ���������һ��������������������ɫ��ͬ����С����ʤ������С����ʤ����������״ͼ���б��ķ����ֱ����С����С����ʤ�ĸ��ʣ���˵�������Ϸ�����˫����ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB��90����BDƽ�֡�ABC��������O��ʹ�õ�O�ڱ�AB�ϣ��ҡ�O����B��D���㣻��֤��AC���O���У����߹���ͼ��������ͼ�ۼ�����д������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ4����������ABCDEF�Ķ���B��C�ֱ���������AMNP�ı�AM��MN�ϣ�CD��PN���ڵ�H����HN�ij�Ϊ_____
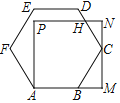
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У���
�У���![]() ������Ϊ��
��������![]() ��
��![]() ������
������![]() ��������
��������![]() ��
��![]() ������C��������
������C��������![]() ��
��![]() ����
����
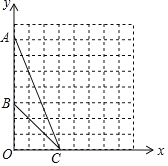
��1����ͼ������![]() �����Բ(���ø�ͼȷ��Բ��)��
�����Բ(���ø�ͼȷ��Բ��)��
��2��Բ������Ϊ _____�����Բ�뾶![]() Ϊ _____��
Ϊ _____��
��3������![]() �������������һ��
�������������һ��![]() ����
����![]() �����
�����![]() ������Ϊ _____��
������Ϊ _____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A����C�ڷ���������y��![]() ��k��0��x��0����ͼ���ϣ�AB��x���ڵ�B��OC��AB�ڵ�D����CD��OD������AOD����BCD�������Ϊ__��
��k��0��x��0����ͼ���ϣ�AB��x���ڵ�B��OC��AB�ڵ�D����CD��OD������AOD����BCD�������Ϊ__��
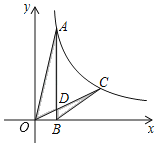
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����F������ABCD�Ķ���A��������A��D��B��1cm/s���ٶ������˶�����B��ͼ2�ǵ�F�˶�ʱ����FBC�����y��cm2����ʱ��x��s���仯�Ĺ�ϵͼ����a��ֵΪ��������

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ǵ��ϲ���ּ���һ�������˶�����������ʱ����Ҫ����ͬƵ˦�����ӣ�������˦����ߴ�ʱ������״�ɽ��ƿ���������.��ͼ��С����С��˦���ӵ���ߴ�ʱ��ʾ��ͼ�����������ӵ���֮��ľ���Ϊ![]() �������ĸ߶�Ϊ
�������ĸ߶�Ϊ![]() ����С����������λ��Ϊԭ�㣬����ƽ��ֱ������ϵ.
����С����������λ��Ϊԭ�㣬����ƽ��ֱ������ϵ.
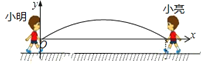
��1��������Ϊ![]() ��С��վ�����ӵ����·����Ҿ�С���������ֵ��Ҳ�
��С��վ�����ӵ����·����Ҿ�С���������ֵ��Ҳ�![]() ��ʱ�����Ӹպ�ͨ��С���ͷ��������������Ӧ�������ߵı���ʽ��
��ʱ�����Ӹպ�ͨ��С���ͷ��������������Ӧ�������ߵı���ʽ��
��2��������Ϊ![]() ��С��Ҳվ�����ӵ����·�.
��С��Ҳվ�����ӵ����·�.
�ٵ�С���ھ�С���������ֵ����![]() ��ʱ������������С����ͷ����˵�����ɣ�
��ʱ������������С����ͷ����˵�����ɣ�
����С����С����������֮���ˮƽ����Ϊ![]() ��Ϊ��֤���Ӳ�����С����ͷ������
��Ϊ��֤���Ӳ�����С����ͷ������![]() ��ȡֵ��Χ.���ο����ݣ�
��ȡֵ��Χ.���ο����ݣ�![]() ȡ3.16��
ȡ3.16��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com