
【题目】甲、乙两人各自加工相同数量的零件,甲先开始工作,中途因故停机检修1小时,重新工作时依旧按照原来的工作效率加工零件,如图是甲、乙两人在整个过程中各自加工的零件个数y(个)与甲工作时间x(时)之间的函数图象.
(1)图中m= ,a= .
(2)求重新工作后甲加工的零件个数y与x之间的函数关系式.
(3)求乙工作期间两人加工的零件个数相差100个时x的值.
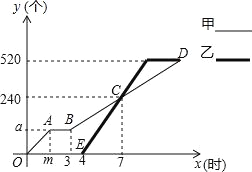
【答案】(1)2;80;(2)y=40x-40;(3)乙工作期间两人加工的零件个数相差100个时x的值是4.5小时或9.5小时.
【解析】
试题分析:(1)根据题意列方程即可得到结论;
(2)设y与x之间的函数关系式为y=kx+b,列方程组即可得到结论;
(3)设直线CE的函数关系式为y=kx+b,求得直线CE的函数关系式为y=80x-320,根根据题意列方程即可得到结论.
试题解析:(1)m=3-1=2,
根据题意得:![]() ,
,
解得:a=80.
(2)设y与x之间的函数关系式为y=kx+b,
∴![]() ,
,
∴![]() ,
,
∴y与x之间的函数关系式为y=40x-40;
(3)设直线CE的函数关系式为y=kx+b,
∴![]() ,
,
∴![]() ,
,
∴直线CE的函数关系式为y=80x-320,
根据题意得:(80x-320)-(40x-40)=100,
解得:x=![]() =4.5,或x=
=4.5,或x=![]() =9.5.
=9.5.
答:乙工作期间两人加工的零件个数相差100个时x的值是4.5小时或9.5小时.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】对称轴平行于y轴的抛物线的顶点为点(2,3)且抛物线经过点(3,1),那么抛物线解析式是( )
A. y=﹣2x2+8x+3 B. y=﹣2x2﹣8x+3 C. y=﹣2x2+8x﹣5 D. y=﹣2x2﹣8x+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小毅和小明同时从学校出发到科技馆参加活动,小毅每小时走6千米,小明每小时走8千米,走了1小时后,小明忘带材料返回学校取材料,立即按原路去追小毅.小明几小时追上小毅?
查看答案和解析>>
科目:初中数学 来源: 题型:
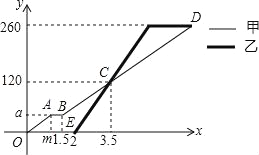
【题目】甲、乙两台机器各自加工相同数量的零件,工作时工作效率不变,甲机器先开始工作,中途停机检修了0.5小时.如图是甲、乙两台机器在整个工作过程中各自加工的零件个数y(个)与甲机器工作时间x(时)之间的函数图象.
(1)求图中m和a的值.
(2)机器检修后,求甲加工的零件个数y与x之间的函数关系式.
(3)在乙机器工作期间,求两台机器加工的零件个数相差50个时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com