
【题目】已知x1,x2是关于x的一元二次方程x2+2(m-3) x+m2+1=0的两个根.
(1)当m取何值时,方程有两个不相等的实数根?
(2)若以x1,x2为对角线的菱形边长是![]() ,试求m的值.
,试求m的值.
【答案】(1)m<![]() 时,方程有两个不相等的实数根;(2)m的值为1.
时,方程有两个不相等的实数根;(2)m的值为1.
【解析】
(1)若方程有两个不相等的实数根,则△=b24ac>0,得到关于m的不等式,求解即可;
(2)由根与系数的关系得出x1+x2=2(m3),x1x2=m2+1.根据菱形的对角线互相垂直平分的性质以及勾股定理得出(![]() x1)2+(
x1)2+(![]() x2)2=3,整理得出关于m的方程,解方程即可.
x2)2=3,整理得出关于m的方程,解方程即可.
(1)由题意得△=[2(m3)]24(m2 +1)=3224m,
要使方程有两个不相等的实数根,则△>0,即3224m>0,
解得m<![]() ,
,
即m<![]() 时,方程有两个不相等的实数根;
时,方程有两个不相等的实数根;
(2)∵x1,x2是关于x的一元二次方程x2+2(m3)x+m2+1=0的两个根,
∴x1+x2=2(m3),x1·x2=m2+1.
∵x1,x2为菱形的对角线,且菱形的对角线互相垂直平分,
∴(![]() x1)2+(
x1)2+(![]() x2)2=3,
x2)2=3,
∴x12+x22=12,
∴(x1+x2)22x1·x2=12,
∴[2(m3)]22(m2+1)=12,
∴m212m+11=0,解得:m1=1,m2=11,
∵m<![]() ,
,
∴m2=11不合题意,舍去,
∴m的值为1.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知函数y1=-![]() x2 和反比例函数y2的图象有一个交点是 A(
x2 和反比例函数y2的图象有一个交点是 A(![]() ,-1).
,-1).
(1)求函数y2的解析式;
(2)在同一直角坐标系中,画出函数y1和y2的图象草图;
(3)借助图象回答:当自变量x在什么范围内取值时,对于x的同一个值,都有y1<y2?
查看答案和解析>>
科目:初中数学 来源: 题型:
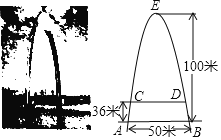
【题目】如图所示是某斜拉索大桥,主索塔呈抛物线,主索塔底部在水面部分的宽度AB=50米,主索塔的最高点E距水面的垂直距离为100米,桥面CD距水面的咨度为36米,则桥的宽度CD_____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]()
(1)求证:无论k为何值,方程总有实数根;
(2)若等腰△ABC的一边长为2,另两边的长为这个方程的两个实数根,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克![]() 元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克
元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克![]() 元,经试销发现,销售量
元,经试销发现,销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图是
(元)符合一次函数关系,如图是![]() 与
与![]() 的函数关系图象.
的函数关系图象.
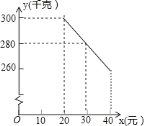
![]() 求
求![]() 与
与![]() 的函数解析式(也称关系式);
的函数解析式(也称关系式);
![]() 设该水果销售店试销草莓获得的利润为
设该水果销售店试销草莓获得的利润为![]() 元,求
元,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用指定的方法解下列方程:
(1)4(x﹣1)2﹣36=0(直接开平方法);
(2)2x2﹣5x+1=0 (配方法)
(3)(x+1)(x﹣2)=4(公式法);
(4)2(x+1)﹣x(x+1)=0(因式分解法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(![]() ),B(
),B(![]() ),C(
),C(![]() )三点.
)三点.
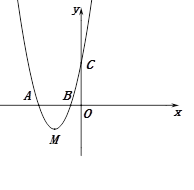
(1)求抛物线的解析式;
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标;
(3)设点M是抛物线的顶点,试判断抛物线上是否存在点H满足![]() ?若存在,请求出点H的坐标;若不存在,请说明理由.
?若存在,请求出点H的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
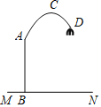
【题目】如图,一款落地灯的灯柱AB垂直于水平地面MN,高度为1.6米,支架部分的形为开口向下的抛物线,其顶点C距灯柱AB的水平距离为0.8米,距地面的高度为2.4 米,灯罩顶端D距灯柱AB的水平距离为1.4米,则灯罩顶端D距地面的高度为______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
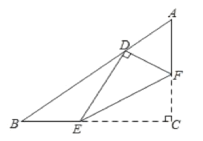
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则AD的长为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com