
【题目】(1)问题探究
①如图1,在直角![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,则
,则![]() 的最小值为_________.
的最小值为_________.
②如图2,在等腰直角![]() 中,
中,![]() ,若
,若![]() ,求边
,求边![]() 的长度(用含
的长度(用含![]() 的代数式表示);
的代数式表示);
(2)问题解决
③如图3,在等腰直角![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,若点
的中点,若点![]() 是
是![]() 边上一点,试求
边上一点,试求![]() 的最小值.
的最小值.

【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]()
【解析】
(1)①如图1中,作BE⊥AC于E.解直角三角形求出BE,根据垂线段最短即可解决问题.
②利用勾股定理即可解决问题.
(2)如图3中,作AH⊥AC,PE⊥AH于E,DF⊥AH于F交AB于T.因为DP+![]() PA=DP+PE,根据垂线线段最短可知,当点E与F重合时,PD+
PA=DP+PE,根据垂线线段最短可知,当点E与F重合时,PD+![]() PA的值最小,最小值为DF的长.
PA的值最小,最小值为DF的长.
(1)①如图1中,作BE⊥AC于E.
在Rt△ABC中,∵∠ABC=90°,AC=5,BC=3,
∴AB=![]() =4,
=4,
∵S△ABC=![]() ACBE=
ACBE=![]() ABBC,
ABBC,
∴BE=![]() =
=![]() ,
,
根据垂线段最短可知当BP与BE重合时,PB的值最小,最小值为![]() ,
,
故答案为![]() .
.
②如图2中,
∵∠B=90°,AB=BC,
∴AB2+BC2=AC2,
∴AB2=![]() a2,
a2,
∴AB=![]() a或-
a或-![]() a(舍弃),
a(舍弃),
∴AB=![]() a.
a.
(2)如图3中,作AH⊥AC,PE⊥AH于E,DF⊥AH于F交AB于T.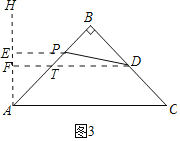
∵△ABC是等腰直角三角形,AC=2![]() ,
,
∴AB=BC=2,∠BAC=∠C=45°,
∵BD=CD=1,
∵DF⊥AH,AC⊥AH,
∴DF∥AC,
∴∠BTD=∠BAC=45°,∠BDT=∠C=45°,
∴∠BTD=∠BDT,
∴BT=BD=AT=1,DT=![]() ,
,
∵AH⊥AC,∠BAC=45°,
∴∠HAC=90°,∠HAT=45°,
∴AF=TF=![]() ,
,
∴PE=![]() PA,
PA,
∴DP+![]() PA=DP+PE,
PA=DP+PE,
根据垂线线段最短可知,当点E与F重合时,PD+![]() PA的值最小,最小值为DF的长=
PA的值最小,最小值为DF的长=![]() +
+![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】探索与发现
探索:如图,在直角坐标系中,正方形ABCO的点B坐标(4,4),点A、C分别在y轴、x轴上,对角线AC上一动点E,连接BE,过E作DE⊥BE交OC于点D.

(1)证明:BE=DE.
小明给出的思路为:过E作y轴的平行线交AB、x轴于点F、H.请完善小明的证明过程.
(2)若点D坐标为(3,0),则点E坐标为 .
若点D坐标为(a,0),则点E坐标为 .
发现:在直角坐标系中,点B坐标(5,3),点D坐标(3,0),找一点E,使得△BDE为等腰直角三角形,直接写出点E坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是____.
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④AC2=CQCB,其中结论正确的是____.
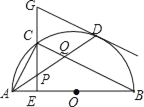
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果绘制成了如图的统计图.在这20位同学中,本学期购买课外书的花费的众数和中位数分别是( )

A. 50,50 B. 50,30 C. 80,50 D. 30,50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的方程
的方程![]() 有增根,则
有增根,则![]() 的值为__________.
的值为__________.
【答案】2
【解析】方程两边都乘(x2),得
x+x2=a,即a=2x2.
分式方程的增根是x=2,
∵原方程增根为x=2,
∴把x=2代入整式方程,得a=2,
故答案为:2.
点睛:本题考查了分式方程的增根,增根是分式方程化为整式方程后产生的使分式方程的分母为0的根.把增根代入化为整式方程的方程即可求出a的值.
【题型】填空题
【结束】
17
【题目】反比例函数y=![]() 的图象经过点(1,6)和(m,-3),则m= .
的图象经过点(1,6)和(m,-3),则m= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()
MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()

A. BP是∠ABC的平分线B. AD=BDC. ![]() D. CD=
D. CD=![]() BD
BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.

(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题背景)
在平行四边形ABCD中,∠BAD=120°,AD=nAB,现将一块含60°的直角三角板(如图)放置在平行四边形ABCD所在平面内旋转,其60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB、AD于点E、F(不包括线段的端点).
(发现)
如图1,当n=1时,易证得AE+AF=AC;
(类比)
如图2,过点C作CH⊥AD于点H,
(1)当n=2时,求证:AE=2FH;
(2)当n=3时,试探究AE+3AF与AC之间的等量关系式;
(延伸)
将60°角的顶点移动到平行四边形ABCD对角线AC上的任意点Q,其余条件均不变,试探究:AE、AF、AQ之间的等量关系式(请直接写出结论).



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com