
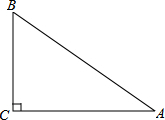
 如图,在△ABC中,∠C=90°,BC=6,AC=8,AB=10.
如图,在△ABC中,∠C=90°,BC=6,AC=8,AB=10.分析 (1)作∠A和∠ACB的角平分线,则它们的交点即为点P;
(2)根据角平分线的性质可说明点P到△ABC三边的距离相等;
(3)根据直角三角形内切圆的半径等于两直角边的和与斜边差的一半进行计算.
解答 解:(1)如图,点P为所作;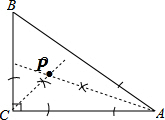
(2)因为点P为△ABC内角的平分线,
所以点P到△ABC三边的距离相等;
(3)设△ABC的内切圆的半径为r,则点P到△ABC三边的距离为r,
而r=$\frac{6+8-10}{2}$=2,
所以点P到△ABC三边的距离为2.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了三角形的内心.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com