练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11、如图（1）、图（2）都是轴对称图形，图（1）有
    2
    条对称轴，图（2）有
    2
    条对称轴
    分析：根据对称轴的定义：如果一个图形沿着一条直线对折，两侧的图形能完全重合，这个图形就是轴对称图形．折痕所在的这条直线叫做对称轴．依此对连心园、长方形图形进行判断．
    解答：解：图（1）、图（2）都是轴对称图形，图（1）有2条对称轴，图（2）有2条对称轴
    故答案为：2，2．
    点评：本题主要考查了轴对称图形的对称轴的定义．同时要熟记一些常见图形的对称轴条数．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：初中数学　三点一测丛书　八年级数学　下　（江苏版课标本） 江苏版 题型：047

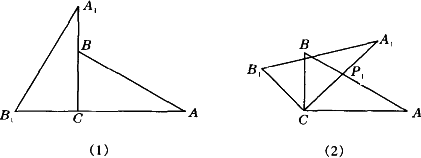
    将两块含30°角且大小相同的直角三角板如图摆放．

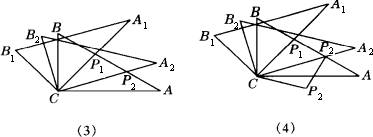
    (1)将图(1)中△A1B1C绕点C顺时针旋转45°得图(2)，点P1是A1C与AB的交点，求证：CP1＝AP1；

    (2)将图(2)中△A1B1C绕点C顺时针旋转30°到△A2B2C(如图(3))，P2是A2C与AB的交点，线段CP1与P1P2之间存在一个确定的等量关系，请你写出这个关系式并说明理由；

    (3)将图(3)中线段CP1绕点C顺时针旋转60°到CP3(如图(4))，连结P3P2，求证：P3P2⊥AB．

    查看答案和解析>>

    科目：初中数学 来源：2006年初中数学总复习下册 题型：044

    将两块含30°角且大小相同的直角三角板如图1摆放．

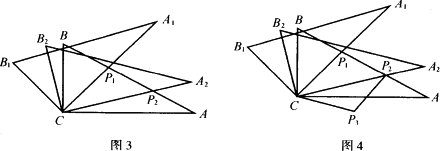
    (1)将图1中△A1B1C绕点C顺时针旋转45°得图2，点P是A1C与AB的交点，求证：CP1＝AP1；

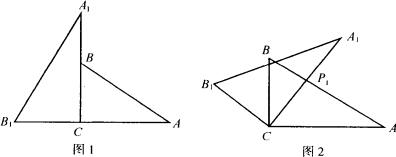
    (2)将图2中△A1B1C绕点C顺时针旋转30°到△A2B2C(如图3)，P2是A2C与AB的交点，线段CP1与P1P2之间存在一个确定的等量关系，请你写出这个关系式并说明理由；

    (3)将图3中线段CP1绕点C顺时针旋转60°到CP3(如图4)，连结P3P2，求证：P3P2⊥AB．

    查看答案和解析>>

    科目：初中数学 来源：2010年中考数学考前知识点回归＋巩固 专题13 二次函数（解析版） 题型：解答题

    如图1，在Rt△ABC中，∠C=90°，BC=8厘米，AC=12厘米，点D在AC上，CD=3厘米．点P、Q分别由A、C两点同时出发，点P沿AC方向向点C匀速移动，速度为每秒是k厘米；点Q沿CB方向向点B匀速移动，速度为每秒1厘米．设运动的时间为x秒（0＜x＜8），△DCQ的面积为y1平方厘米，△PCQ的面积为y2平方厘米．
    （1）求y1与x的函数关系，并在图2中画出y1的图象；
    （2）如图2，y2的图象是抛物线的一部分，其顶点坐标是（4，12），求k的值和y2与x的函数关系；
    （3）在图2中，设y1与y2的图象的交点为M，点G是x轴正半轴上一点（0＜OG＜6），过G作EF垂直于x轴，分别与y1、y2的图象交于点E、F．求△OMF面积的最大值．
    ①说出线段EF的长在图1中所表示的实际意义；
    ②求△OMF面积的最大值．

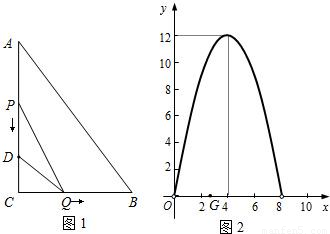
    查看答案和解析>>

    科目：初中数学 来源：2009年江苏省苏州市张家港市中考网上阅卷适应性考试数学试卷（解析版） 题型：解答题

    如图1，在Rt△ABC中，∠C=90°，BC=8厘米，AC=12厘米，点D在AC上，CD=3厘米．点P、Q分别由A、C两点同时出发，点P沿AC方向向点C匀速移动，速度为每秒是k厘米；点Q沿CB方向向点B匀速移动，速度为每秒1厘米．设运动的时间为x秒（0＜x＜8），△DCQ的面积为y1平方厘米，△PCQ的面积为y2平方厘米．
    （1）求y1与x的函数关系，并在图2中画出y1的图象；
    （2）如图2，y2的图象是抛物线的一部分，其顶点坐标是（4，12），求k的值和y2与x的函数关系；
    （3）在图2中，设y1与y2的图象的交点为M，点G是x轴正半轴上一点（0＜OG＜6），过G作EF垂直于x轴，分别与y1、y2的图象交于点E、F．求△OMF面积的最大值．
    ①说出线段EF的长在图1中所表示的实际意义；
    ②求△OMF面积的最大值．

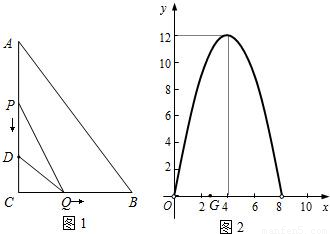
    查看答案和解析>>

    科目：初中数学 来源：期中题 题型：解答题

    如图①，是公交公司某条公交线路的收支差额y（即票价总收入减去运营成本）与乘客量x之间的函数图象。
    目前这条线路亏损，为了扭亏，有关部门举行提高票价听证会
    乘客代表认为：公交公司应改善管理，降低运营成本，以此举实现扭亏。
    公交公司认为：运营成本难以下降，公司已尽力，应适当提高票价才能扭亏。
    根据这两种意见，可以把图①分别改画成图②和图③。
    （1）说明图①中点A、点B的实际意义；
    （2）你认为图②和图③两个图象中，反映乘客的意见是图         ，反映公司意见的是图         （3）如果公交公司采用适当提高票价，又减少成本的办法实现扭亏为赢，请你在图④中画出符合这种办法的y与x大致函数关系的图象。

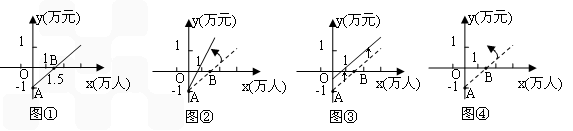
    查看答案和解析>>

    同步练习册答案