
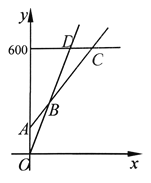
【题目】某乒乓球馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:①金卡售价600元/张,每次凭卡不再收费;②银卡售价150元/张,每次凭卡另收10元;暑期普通票正常出售,两种优惠卡仅限暑期使用,不限次数.设打乒乓x次时,所需总费用为y元.
(1)分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
(2)在同一个坐标系中,若三种消费方式对应的函数图像如图所示,请根据函数图像,写出选择哪种消费方式更合算.
【答案】(1)![]() ,
,![]() ;(2)当打球次数不足15次时,选择普通票最合算,当打球次数介于15次到45次之间时,选择银卡最合算,当打球次数超过45次时,选择金卡最合算,当打球次数恰为15次时,选择普通票或银卡同为最合算,当打球次数恰为45次时,选择金卡或银卡同为最合算.
;(2)当打球次数不足15次时,选择普通票最合算,当打球次数介于15次到45次之间时,选择银卡最合算,当打球次数超过45次时,选择金卡最合算,当打球次数恰为15次时,选择普通票或银卡同为最合算,当打球次数恰为45次时,选择金卡或银卡同为最合算.
【解析】
(1)根据银卡售价150元/张,每次凭卡另收10元,以及旅游馆普通票价20元/张,设游泳x次时,分别得出所需总费用为y元与x的关系式即可;
(2)利用函数交点坐标求法分别得出即可,利用点的坐标以及结合得出函数图象得出答案.
解:(1)选择银卡消费时,y与x之间的函数关系式为:![]()
选择普通票消费时,y与x之间的函数关系式为:![]()
(2)根据题意,分别求出A(0,150)、B(15,300)、C(45,600)
∴当打球次数不足15次时,选择普通票最合算,当打球次数介于15次到45次之间时,选择银卡最合算,当打球次数超过45次时,选择金卡最合算,当打球次数恰为15次时,选择普通票或银卡同为最合算,当打球次数恰为45次时,选择金卡或银卡同为最合算.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论为( )
,其中正确结论为( )
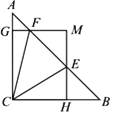
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,AD=![]() ,将矩形ABCD绕着顶点B顺时针旋转,得到矩形EBGF,顶点A、D、C分别与点E、F、G对应(点D与点F不重合).如果点D、E、F在同一条直线上,那么线段DF的长是____.(用含
,将矩形ABCD绕着顶点B顺时针旋转,得到矩形EBGF,顶点A、D、C分别与点E、F、G对应(点D与点F不重合).如果点D、E、F在同一条直线上,那么线段DF的长是____.(用含![]() 的代数式表示)
的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某底面为圆形的古塔剖面和山坡的剖面在同一平面上,古塔EF(F为塔底的中心)与地面BD垂直,古塔的底面直径CD=8米,BC=10米,斜坡AB=26米,斜坡坡面AB的坡度i=5:12,在坡脚的点A处测得古塔顶端点E的仰角∠GAE=47°,则古塔EF的高度约( )(参考数据:sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)
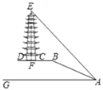
A. 27.74米B. 30.66米C. 35.51米D. 40.66米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC为等边三角形,点D为直线BC上一动点(点D不与B、C重合).以
AD为边作菱形ADEF,使∠DAF=60°,连接CF.
⑴如图1,当点D在边BC上时,
求证:∠ADB=∠AFC;②请直接判断结论∠AFC=∠ACB+∠DAC是否成立;
⑵如图2,当点D在边BC的延长线上时,其他条件不变,结论∠AFC=∠ACB+∠DAC是否成立?请写出∠AFC、∠ACB、∠DAC之间存在的数量关系,并写出证明过程;
⑶如图3,当点D在边CB的延长线上时,且点A、F分别在直线BC的异侧,其他条件不变,请补全图形,并直接写出∠AFC、∠ACB、∠DAC之间存在的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为
的坐标为![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以每秒
轴以每秒![]() 个单位的速度向上移动,且过点
个单位的速度向上移动,且过点![]() 的直线
的直线![]() 也随之移动,如果点
也随之移动,如果点![]() 关于
关于![]() 的对称点落在坐标轴上,没点
的对称点落在坐标轴上,没点![]() 的移动时间为
的移动时间为![]() ,那么
,那么![]() 的值可以是___.
的值可以是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
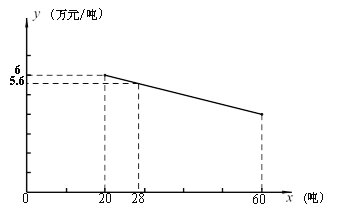
【题目】某工厂生产一种产品,当生产数量至少为20吨,但不超过60吨时,每吨的成本![]() (万元/吨)与生产数量
(万元/吨)与生产数量![]() (吨)之间是一次函数关系,其图像如图所示.
(吨)之间是一次函数关系,其图像如图所示.
(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)如果每吨的成本是4.8万元,求该产品的生产数量;
(3)当生产这种产品的总成本是200万元时,求该产品的生产数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 点,经过点
点,经过点![]() 的抛物线
的抛物线![]() 上有一动点
上有一动点![]() ,且点
,且点![]() 在直线
在直线![]() 的下方.
的下方.
(1)平移直线![]() 经过点
经过点![]() ,得到直线
,得到直线![]() ,点
,点![]() 为直线
为直线![]() 上一个动点,连接
上一个动点,连接![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的最小值.
的最小值.
(2)平移直线![]() 经过原点,得到直线
经过原点,得到直线![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() 点横坐标为6,点
点横坐标为6,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,当
轴上,当![]() 时,抛物线上是否存在点
时,抛物线上是否存在点![]() ,使四边形
,使四边形![]() 是矩形?如果存在,请求出点
是矩形?如果存在,请求出点![]() 的坐标,如果不存在,请说明理由.
的坐标,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF与⊙O相切于点C,点A为⊙O上异于点C的一动点,⊙O的半径为4,AB![]() EF于点B,设
EF于点B,设![]() ACF=α(0°<α<180°).
ACF=α(0°<α<180°).
(1)若α=![]() ,求证:四边形OCBA为正方形;
,求证:四边形OCBA为正方形;
(2)若AC―AB=1,求AC的长;
(3)当AC―AB取最大值时,求α的度数.
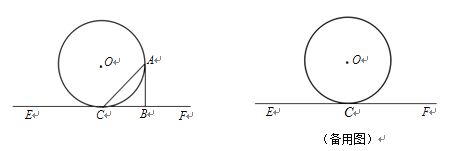
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com