
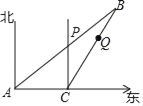
【题目】如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿某一方向直航140海里的海岛B,其速度为14海里/小时;乙船速度为20海里/小时,先沿正东方向航行3小时后,到达C港口接旅客,停留1小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
(1)求海岛B到航线AC的距离;
(2)甲船在航行至P处,发现乙船在其正东方向的Q处,问此时两船相距多少?
【答案】(1)海岛B到航线AC的距离为50![]() 海里;(2)两船相距12海里.
海里;(2)两船相距12海里.
【解析】
(1)过点B作BD⊥AE于D,在Rt△BCD中,∠BCD=60°,设CD=x,可得BD=![]() x,在Rt△BDA中,根据勾股定理可得方程1402=(60+x)2+(
x,在Rt△BDA中,根据勾股定理可得方程1402=(60+x)2+(![]() x)2,解方程求得x的值,即可求得BD的长;(2)设运动时间为t,则AP=14t,CQ=20(t﹣4),BC=100,由题意可知PQ∥AC,由平行线分线段成比例定理可得
x)2,解方程求得x的值,即可求得BD的长;(2)设运动时间为t,则AP=14t,CQ=20(t﹣4),BC=100,由题意可知PQ∥AC,由平行线分线段成比例定理可得![]() ,代入数值求得t值,即可求得AP、PB的长;再由△BPQ∽△BAC,根据相似三角形的性质可得
,代入数值求得t值,即可求得AP、PB的长;再由△BPQ∽△BAC,根据相似三角形的性质可得![]() ,代入数据即可求得PQ的长.
,代入数据即可求得PQ的长.
(1)过点B作BD⊥AE于D,
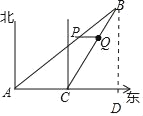
由题意可知AC=60,AB=140,
在Rt△BCD中,∠BCD=60°,
设CD=x,则BD=![]() x,
x,
∵在Rt△BDA中,∠BDA=90°
∴AD2+BD2=AB2,得1402=(60+x)2+(![]() x)2
x)2
x2+30x﹣4000=0,
∴x=50或﹣80(舍弃),
∴BD=50![]() .
.
∴海岛B到航线AC的距离为50![]() 海里;
海里;
(2)设运动时间为t,则AP=14t,CQ=20(t﹣4),BC=100,
若点Q在点P的正东方向,则PQ∥AC,
∴![]() =
=![]() ,即:
,即:![]() =
=![]() ,得t=8,
,得t=8,
∴AP=112,PB=140-112=28.
由∵△BPQ∽△BAC,
∴![]() =
=![]() ,即:
,即:![]() =
=![]() ,
,
得PQ=12.
∴两船相距12海里.


科目:初中数学 来源: 题型:
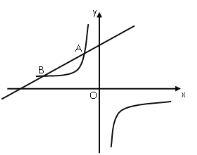
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
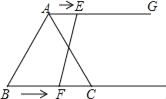
【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=______s时,以A、C、E、F为顶点四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业为了提高工人劳动的积极性,决定对工人的月工资进行调整.已知该企业有 n 名工人,调整后的月工资 y(元)与调整前的月工资 x(元)满足一次函数关系,如下表:

(1)求 y 与 x 的函数关系式;
(2)若某名工人调整前月工资是4800元,那么调整后这名工人月工资增加了多少元?
(3)这 ![]() 名工人调整前、后的平均月工资分别为
名工人调整前、后的平均月工资分别为![]() ,
,![]() ,猜想
,猜想![]() 与
与![]() 的关系式,并写出推导过程.
的关系式,并写出推导过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AC⊥BC于C,BC=a,CA=b,AB=c,下列图形中⊙O与△ABC的某两条边或三边所在的直线相切,则⊙O的半径为![]() 的是( )
的是( )
A. 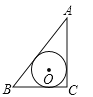 B.
B. 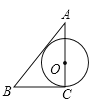
C. 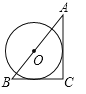 D.
D. 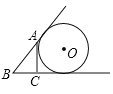
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两条线段AC和BC,连接AB,分别以AB、BC为底边向上画等腰△ABD和等腰△BCE,∠ADB=∠BEC=α.
(1)如图1,当α=60°时,求证:△DBE≌△ABC;
(2)如图2,当α=90°时,且BC=5,AC=2.
①求DE的长;
②如图3,将线段CA绕点C旋转,点D也随之运动,请求出C,D两点之间距离的取值范围.
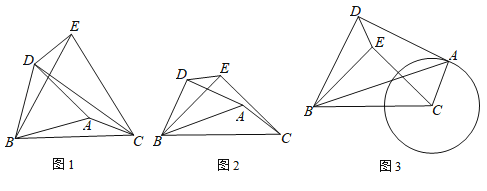
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,不正确的是( )
A. 直角边长分别是6、4和4.5、3的两个直角三角形相似 B. 底角为40°的两个等腰三角形相似
C. 一个锐角为30°的两个直角三角形相似 D. 有个角为30°的两个等腰三角形相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新课程改革十分关注学生的社会实践活动,小明在一次社会实践活动中负责了解他所居住的小区500户居民的家庭月人均收入情况,他从中随机调查了40户居民家庭的“家庭月人均收入情况”(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).
分组 | 频数 | 占比 |
1000≤x<2000 | 3 | 7.5% |
2000≤x<3000 | 5 | 12.5% |
3000≤x<4000 | a | 30% |
4000≤x<5000 | 8 | 20% |
5000≤x<6000 | b | c |
6000≤x<7000 | 4 | 10% |
合计 | 40 | 100% |
(1)频数分布表中,a= ,b= ,C= ,请根据题中已有信息补全频数分布直方图;
(2)观察已绘制的频数分布直方图,可以看出组距是 ,这个组距选择得 (填“好”或“不好”),并请说明理由.
(3)如果家庭人均月收入“大于3000元不足6000元”的为中等收入家庭,则用样本估计总体中的中等收入家庭大约有 户.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com