
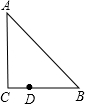
 Rt△ABC中,已知∠C=90°,点D在边BC上,BD=2CD(如图),把线段BD绕着点D逆时针旋转m(0<m<180°)后,使得点B恰好落在边AC上,那么m=120°.
Rt△ABC中,已知∠C=90°,点D在边BC上,BD=2CD(如图),把线段BD绕着点D逆时针旋转m(0<m<180°)后,使得点B恰好落在边AC上,那么m=120°. 分析 根据旋转的性质得∴DB′=DB,∠B′DB=m,由于BD=2CD,则DB′=2CD,根据含30度的直角三角形三边的关系得∠CB′D=30°,再利用互余计算出∠CDB′=60°,然后利用邻补角的定义得到∠B′DB=120°.
解答 解:当点B的对应点B′落在AC边上,如图,
∵线段BD绕着点D逆时针旋转m(0<m<180°)后,使得点B恰好落在边AC上,
∴DB′=DB,∠B′DB=m,
∵BD=2CD,
∴DB′=2CD,
∵∠C=90°,
∴∠CB′D=30°,
∴∠CDB′=60°,
∴∠B′DB=180°-60°=120°,即m=120°.
故答案为:120°.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了含30度的直角三角形三边的关系和等腰三角形的性质.


科目:初中数学 来源: 题型:填空题
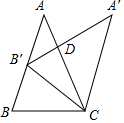 如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转后得到△A'B'C,设∠A'CB=a,点B'在AB上,则∠ADA'=4α-360°(用含a的式子表示)
如图,在△ABC中,AB=AC,将△ABC绕点C顺时针旋转后得到△A'B'C,设∠A'CB=a,点B'在AB上,则∠ADA'=4α-360°(用含a的式子表示)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com