
���������� �֣�С����С����һ����¥ǰ�п�¥����ߣ�С��˵������¥����
�֣�С����С����һ����¥ǰ�п�¥����ߣ�С��˵������¥���� �㣡��С��ȴ����ΪȻ����
�㣡��С��ȴ����ΪȻ���� �㣿�ҿ�û�У���С��˵�����б��£���������һ���������ɣ���
�㣿�ҿ�û�У���С��˵�����б��£���������һ���������ɣ���
��ͼ������ ��ʾ¥�壬С����С����¥�������ѡ
��ʾ¥�壬С����С����¥�������ѡ ��
�� ���㣬ʹ��
���㣬ʹ�� ��
�� ��
�� ��
��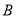 �ĵ���ͬһֱ���ϣ�����Ƥ�ߺͲ���������������ݣ�
�ĵ���ͬһֱ���ϣ�����Ƥ�ߺͲ���������������ݣ�  �ף�
�ף�  �ף�
�ף�  ��
��  ��
��

�� ���������������һ��¥�ߣ�������������ţ�
���������������һ��¥�ߣ�������������ţ�
�� ����ÿ��¥��
����ÿ��¥�� ���㣬��֧��С������С���Ĺ۵��أ���˵�����ɣ�
���㣬��֧��С������С���Ĺ۵��أ���˵�����ɣ�
 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�˽̰��ϲ��4�� ����ͼ�γ��� ��Ԫ���Ծ� ���ͣ������
��֪A��B��C���㶼�������ϣ���A�������϶�Ӧ����Ϊ2����AB��5��BC��3�����C�������϶�Ӧ����Ϊ________.
��6��0��4��10 �����������B��C�������϶�Ӧ�����ֱ�Ϊx��y�� ��AB=5����A�������϶�Ӧ����Ϊ2�� ��|x-2|=5�� ��x=7��-3�� ��BC=3�� ��|y-x|=3�� �ٵ�x=7ʱ��|y-7|=3�� ��y=10��4�� �ڵ�x=-3ʱ��|y+3|=3�� ��y=0��-6�� ���C�������϶�Ӧ����Ϊ��6��0��4��10.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ɽ��ʡ��������У���꼶���ϣ���һ��������ѧ�Ծ� ���ͣ���ѡ��
����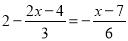 ȥ��ĸ�ã�������
ȥ��ĸ�ã�������
A. 2��2��2x��4��=����x��7�� B. 12��2��2x��4��=��x��7
C. 12��2��2x��4��=����x��7�� D. ���ϴ𰸾�����
C ���������ⷽ�̣� ȥ��ĸ�ã� . ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����ѧ����ĩ��ѧ���������꼶��ѧ�Ծ� ���ͣ���ѡ��
��ͼ��ʾ�ļ���������һЩС�������ɵģ�����������������ͼ�ǣ�������

A.  B.
B.  C.
C. 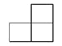 D.
D. 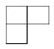
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
�� �֣�������
�֣������� �У�
��  ��
�� 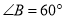 ����
���� ���߶�
���߶� �ϵ�һ�����㣮
�ϵ�һ�����㣮
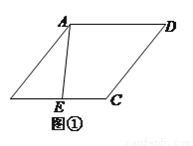
�� ����ͼ�٣���
����ͼ�٣��� ����Сֵ��
����Сֵ��
��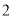 ����ͼ�ڣ���
����ͼ�ڣ��� Ҳ��
Ҳ�� ���ϵ�һ�����㣬��
���ϵ�һ�����㣬�� ����
���� ����Сֵ��
����Сֵ��
�� ����ͼ�ۣ���
����ͼ�ۣ���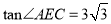 �����������ڲ�����һ��
�����������ڲ�����һ�� ��ʹ�õ�
��ʹ�õ�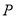 �ֱ�
�ֱ� ����
���� ����
���� �ľ���֮����С�����㻭�������ĵ�
�ľ���֮����С�����㻭�������ĵ� ������������Сֵ��
������������Сֵ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��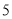 �֣����㣺
�֣����㣺
 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��������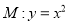 ����ƽ��
����ƽ�� ����λ��������ƽ��
����λ��������ƽ�� ����λ���õ�������
����λ���õ������� ��
��  ��
�� �ύ��
�ύ��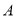 ��
�� ���㣬
���㣬 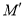 �Ķ����Ϊ
�Ķ����Ϊ ����
���� ������� ����
������� ����

A.  B.
B. 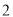 C.
C. 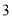 D.
D. 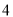
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�꼶��ѧ�²�ڶ�ʮ���� ������ ���ͣ������
ǽ��CD��D����һյ�ƣ���ͼ����С��վ��A���������Ӱ����������ȣ���Ϊ1.6m������ǽ����1m��B��ʱ����Ӱ�Ӹպ�����A�㣬����������ľ���CD=_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰����꼶�²���ѧ�������ཻ����ƽ���ߵ�Ԫ���� ���ͣ������
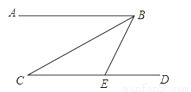
��ͼ����֪AB��CD��BCƽ�֡�ABE����C=34�㣬���BED=________��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com