
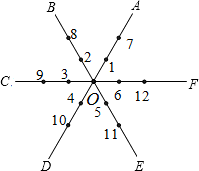
 如图,平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF,从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…,则数字“2012”在
如图,平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF,从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…,则数字“2012”在 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
 10、如图,平面内有公共端点的八条射线OA、OB、OC、OD、OE、OF、OG、OH,从射线OA开始按逆时针方向依次在射线上写上数字1、2、3、4、5、6、7、8、9,….按此规律,数2010在射线( )
10、如图,平面内有公共端点的八条射线OA、OB、OC、OD、OE、OF、OG、OH,从射线OA开始按逆时针方向依次在射线上写上数字1、2、3、4、5、6、7、8、9,….按此规律,数2010在射线( )查看答案和解析>>
科目:初中数学 来源: 题型:
 1、如图,平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF,从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…,则数字“2008”在( )
1、如图,平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF,从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…,则数字“2008”在( )查看答案和解析>>
科目:初中数学 来源: 题型:
 写出数字1,2,3,4,5,6,7,….
写出数字1,2,3,4,5,6,7,….查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF,从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…,则数字“2012”在( )
如图,平面内有公共端点的六条射线OA、OB、OC、OD、OE、OF,从射线OA开始按逆时针依次在射线上写出数字1、2、3、4、5、6、7…,则数字“2012”在( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,平面内有公共端点的五条射线OA,OB,OC,OD,OE,以O为圆心画圆,在第1个圆与射线OA,OB,OC,OD,OE的交点上依次标出数字l,2,3,4,5,在第2个圆与射线OA,OB,OC,OD,OE的交点上依次标出数字6,7,8,9,10以此类推…
如图,平面内有公共端点的五条射线OA,OB,OC,OD,OE,以O为圆心画圆,在第1个圆与射线OA,OB,OC,OD,OE的交点上依次标出数字l,2,3,4,5,在第2个圆与射线OA,OB,OC,OD,OE的交点上依次标出数字6,7,8,9,10以此类推…查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com