
分析 根据有理数加减混合运算法则计算即可.
解答 解:(1)(-3.4)+4.3=0.9;
(2)(-81)-(-29)=-81+29=-52;
(3)(-9)+4+(-5)+8=-14+12=-2;
(4)-5.4+0.2-0.6+0.8=-6+1=-5;
(5)(-1)-$\frac{3}{5}$-(-$\frac{2}{7}$)+$\frac{3}{7}$+(-$\frac{2}{5}$)=-2+1=-1;
(6)4$\frac{3}{4}$+(+3.85)-(-3$\frac{1}{4}$)-(+3.85)=8;
(7)-$\frac{2}{3}$-|-$\frac{3}{4}$|+(-$\frac{1}{3}$)-(-$\frac{1}{4}$)=-1-$\frac{1}{2}$=-$\frac{3}{2}$;
(8)(-1)+(+2)+(-3)+(+4)+…+(-99)+(+100)=50.
点评 本题考查的是有理数的混合运算,掌握有理数加减混合运算法则是解题的关键.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
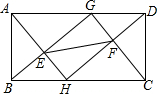 如图,在矩形ABCD中,AB=5,AD=10,点E、F是矩形内两点,BE=DF=3,AE=CF=4,AE的延长线与DF的延长线交于点H,BE的延长线与CF的延长线交于点G,
如图,在矩形ABCD中,AB=5,AD=10,点E、F是矩形内两点,BE=DF=3,AE=CF=4,AE的延长线与DF的延长线交于点H,BE的延长线与CF的延长线交于点G,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD中,AD为⊙O的直径,E为AB上一点将正方形沿EC折叠,点B落在⊙O上的F点.
如图,正方形ABCD中,AD为⊙O的直径,E为AB上一点将正方形沿EC折叠,点B落在⊙O上的F点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com