
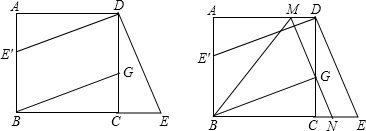
 利用一面墙(墙EF最长可利用25米),用砌37米长的墙的材料围成一个矩形花园ABCD,与围墙平行的一边BC上要预留3米宽的入口(如图中MN所示,不用砌墙).设边AB的长是x米,矩形花园ABCD的面积是y平方米.
利用一面墙(墙EF最长可利用25米),用砌37米长的墙的材料围成一个矩形花园ABCD,与围墙平行的一边BC上要预留3米宽的入口(如图中MN所示,不用砌墙).设边AB的长是x米,矩形花园ABCD的面积是y平方米.分析 (1)设边AB的长是x米,则BC=(40-2x)米.利用矩形的面积公式列出函数关系是即可;
(2)利用配方法求得函数的最大值即可;
(3)根据题意列出不等式,然后解不等式即可求得x的取值范围.
解答 解:(1)设边AB的长是x米,则BC=(37+3-2x)=(40-2x)米.
∴y=(40-2x)x=-2x2+40x.
∴y=-2x2+40x(7.5≤x≤18.5).
(2)y=-2x2+40x
=-2(x2-20x)
=-2(x2-20x+100-100)
=-2[(x-10)2-100]
=-2(x-10)2+200
∴当x=10时,这个矩形花园ABCD的面积y最大,最大值为200平方米.
(3)根据题意得:-2(x-10)2+200≥128.
解得:4≤x≤16.
∵7.5≤x≤18.5,
∴x的取值范围是7.5≤x≤16.
故答案为:7.5≤x≤16.
点评 本题主要考查的是二次函数的应用,根据题意列出关于函数的解析式是解题的关键.


 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
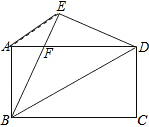 如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com