
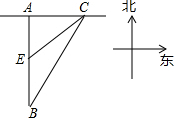
 阅读材料,回答问题
阅读材料,回答问题分析 (1)首先表示出AC=20t,AE=AB-BE=100-40t,再利用勾股定理得出t的值,进而得出答案;
(2)直接表示出FM=FA+AB-BM=130-40t,MD=20$\sqrt{10}$,进而利用勾股定理得出答案.
解答 解:(1)设途中会遇到台风,且最初遇到台风的时间为t小时,此时,轮船位于C处,台风中心移到E处,则有,
AC=20t,AE=AB-BE=100-40t,EC=20$\sqrt{10}$,
在Rt△AEC中,AC2+AE2=EC2,
则(20t)2+(100-40t)2=(20$\sqrt{10}$)2,
整理得:t2-4t+3=0,
解得:t1=1,t2=3,
所以,途中将遇到台风,最初遇到台风的时间为1小时;
(2)设台风抵达D港为t小时,此时台风中心至M点,过D作DF⊥AB,垂足为F,
连接DM,
在Rt△ADF中,AD=60,∠FAD=60°,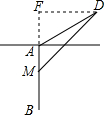
则DF=30$\sqrt{3}$,FA=30,
∵FM=FA+AB-BM=130-40t,MD=20$\sqrt{10}$,
∴(30$\sqrt{3}$)2+(130-40t)2=(20$\sqrt{10}$)2,
整理得:4t2-26t+39=0,
解得:t1=$\frac{13-\sqrt{13}}{4}$,t2=$\frac{13+\sqrt{13}}{4}$,
∴台风抵达D港时间为:$\frac{13-\sqrt{13}}{4}$小时,
因轮船从A处用$\frac{13-\sqrt{13}}{4}$小时到达D港,其速度为:60÷$\frac{13-\sqrt{13}}{4}$≈25.5,
故为使台风抵达D港之前轮船到达D港,轮船至少应提速6海里/时.
点评 此题主要考查了解直角三角形的应用和勾股定理的应用,正确应用勾股定理是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A(m,m+1),B(m+3,m-1)是反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的交点,求:
如图,点A(m,m+1),B(m+3,m-1)是反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的交点,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 羽毛球数n | 100 | 200 | 300 | 400 | 500 | 600 | 1000 | 2000 |
| 优等品数m | 85 | 184 | 261 | 366 | 450 | 552 | 893 | 1804 |
| 优等品率$\frac{m}{n}$ | 0.85 | 0.92 | 0.87 | 0.915 | a | 0.92 | 0.893 | 0.902 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com