
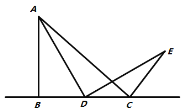
����Ŀ�������ⱳ������ͼ1��ʾ����![]() �У�
��![]() ��
��![]() ����DΪֱ��
����DΪֱ��![]() �ϵĸ����㣨����B��C�غϣ�������
�ϵĸ����㣨����B��C�غϣ�������![]() �����߶�
�����߶�![]() �Ƶ�D��˳ʱ�뷽����ת90����ʹ��A��ת����E������
�Ƶ�D��˳ʱ�뷽����ת90����ʹ��A��ת����E������![]() .
.
�������̽�������D���߶�![]() ���˶���ͨ���۲졢������С���γ������µĽ���˼·������E��
���˶���ͨ���۲졢������С���γ������µĽ���˼·������E��![]() ��ֱ��
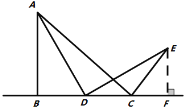
��ֱ��![]() ��F����ͼ2��ʾ��ͨ��֤��
��F����ͼ2��ʾ��ͨ��֤��![]() ______������֤
______������֤![]() ��_____�����Σ��Ӷ����
��_____�����Σ��Ӷ����![]() ______��.
______��.
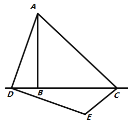
������̽���������D���߶�![]() ���ӳ������˶�����ͼ3��ʾ�����
���ӳ������˶�����ͼ3��ʾ�����![]() �Ķ���.
�Ķ���.
����չ���죩����![]() ������D��ֱ��
������D��ֱ��![]() ���˶�ʱ����
���˶�ʱ����![]() ����ֱ��д��
����ֱ��д��![]() ����Сֵ.
����Сֵ.
ͼ1 ͼ2 ͼ3
���𰸡���1����ADB������ֱ�ǣ�135�㣻��2��45�㣻��3��![]() .
.
��������
��1�������̽������ת�����ʵõ���ADE=90�㣬AD=DE�����ADB+��EDF=��ADB+��DAB=90�㣬�õ���DAB=��EDF�������AAS�õ���DEF�ա�ADB����EF=BD��DF=AB����AB=AC=DF���õ�BD=CF=EF�����CEF�ǵ���ֱ�������Σ��Ӷ��õ���DCE=135�㣻
��2������̽��������E��EG��CD���루1��ͬ������֤��ABD�ա�DGE���õ�BD=GE��AB=DG=BC����BD=CG=GE�����ɵõ�![]() ��
��
��3����չ���죺����D��ֱ��BC���˶�ʱ����BE��CEʱ��BE�ij�������Сֵ���ɣ�2����֪![]() �����BCEΪ����ֱ�������Σ���
�����BCEΪ����ֱ�������Σ���![]() .
.
�⣺��1�������̽����ͼ��
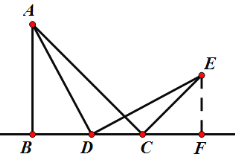
����ת�����ʣ��ã���ADE=90�㣬AD=DE��
���ADB+��EDF=90�㣬
�ߡ�ABC=90�㣬
���ADB+��DAB=90�㣬
���DAB=��EDF��
��EF��BC��
���ABC=��DFE=90�㣬
���ADB�ա�DEF��AAS����
��BD=EF��AB=DF��
��AB=DF=BC��
��BD+DC=DC+CF��
��BD=CF=EF��
���CEF�ǵ���ֱ�������Σ�
���CEF=45�㣬
���DCE=��CEF+��CFE=45��+90��=135�㣻
�ʴ�Ϊ����ADB������ֱ�ǣ�135�㣻
��2������̽������ͼ������E��EG��CD��
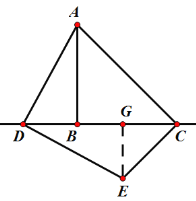
�ߡ�ADE=��ADB+��GDE=90�㣬��ADB+��DAB=90�㣬
���GDE=��DAB��
�ߡ�ABD=��DGE=90�㣬AD=DE��
���ABD�ա�DGE��AAS����
��BD=GE��AB=DG=BC��
��BD+BG=BG+GC��
��CG=BD=GE��
���CEG�ǵ���ֱ�������Σ�
���DCE=45�㣻
��3����չ���죺��ͼ������D��ֱ��BC���˶�ʱ����BE��CEʱ��BE�ij�������Сֵ��
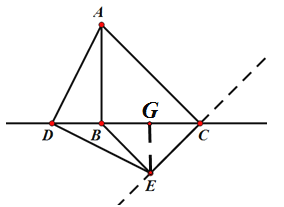
���BEC=90��.
�ɣ�2����֪����DCE=45�㣬
���BCE�ǵ���ֱ�������Σ�
��BE=CE��
��![]() ��
��
��![]() ��
��
��BE����СֵΪ![]() .
.


 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����D�ڡ�ABC�ڣ�BD=BC����DBC=60������E�ڡ�ABC�⣬��BCE=150������ABE=60����
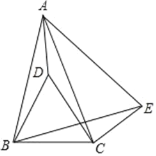
��1����֤����ADB�ա�ADC �� �������ADB�Ķ�����
��2��С��˵��ABE�ǵ��������Σ�С��˵��ABE�ǵȱ������Σ����� ˵����ȷ����˵�����ɣ�
��3������DE����DE��BD��DE=8����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��
��1����ֱ�ߺ�Բ�滭��![]() ��ƽ����
��ƽ����![]() ��������ͼ�ۼ�����д����������֤����
��������ͼ�ۼ�����д����������֤����
��2��������![]() ������ѡȡһ��
������ѡȡһ��![]() ����������
����������![]() ��ѡȡһ��
��ѡȡһ��![]() ��Ҫ��
��Ҫ��![]() Ϊ�۽ǣ�
Ϊ�۽ǣ�
��������![]() ���ҵ�����ʹ��
���ҵ�����ʹ��![]() �ĵ�
�ĵ�![]() ��
��
���![]() ��
��![]() ֮���������ϵ����֤����
֮���������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
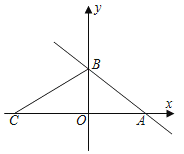
����Ŀ����ͼ��һ�κ���y����![]() x+3��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B��C��x����һ���㣬����BC������ABC��BC���ڵ�ֱ���۵�������A����y����ʱ����C������Ϊ__��
x+3��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B��C��x����һ���㣬����BC������ABC��BC���ڵ�ֱ���۵�������A����y����ʱ����C������Ϊ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
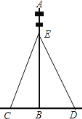
����Ŀ����ͼ��Ϊ��ʹ���߸��ȹ̵Ĵ�ֱ�ڵ��棬���ೣ�������ĸ�˿�����̶������ڸ�˿���Ľ���![]() �ڵ��߸˵�������֮һ��������֪��
�ڵ��߸˵�������֮һ��������֪��![]() �ĸ߶ȾͿ���֪�����߸�
�ĸ߶ȾͿ���֪�����߸�![]() �ĸ߶��ˣ�Ҫ��õ�
�ĸ߶��ˣ�Ҫ��õ�![]() �ĸ߶ȣ���Ҫ������һЩ���ݣ�Ȼ��ͨ������ó���
�ĸ߶ȣ���Ҫ������һЩ���ݣ�Ȼ��ͨ������ó���
������Ƴ�Ҫ�����Ķ���________��
����д������![]() �߶ȵ�˼·��________��
�߶ȵ�˼·��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ͬʱ���������������Գ�����
ͬʱ���������������Գ�����![]() ����ֵ��
����ֵ��![]() �����κ�����ͼ����
�����κ�����ͼ����![]() �����������㣬��������ƽ����Ϊ
�����������㣬��������ƽ����Ϊ![]() ����
����![]() ��ֵ�ǣ� ��
��ֵ�ǣ� ��
A. ![]() ��
��![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������������߶ε��е�����ĶԳƣ���ƽ��ֱ������ϵ�У���������P(x1��y1)��Q (x2��y2)�ĶԳ����ĵ�����Ϊ![]() ����ͼ��
����ͼ��
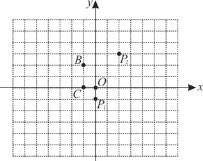
��1����ƽ��ֱ������ϵ�У�����P1(0��-1)��P2(2��3)�ĶԳ������ǵ�A�����A������Ϊ________��
��2����ȡ����![]() ��
��![]() ����һ�������ܴӵ�P1����ʼ���������ڵ�A��B��C��ѭ���Գ�����������һ��������P1���ڵ�A�ĶԳƵ�P2��������������P2���ڵ�B�ĶԳƵ�P3������������������P3���ڵ�C�ĶԳƵ�P4�������Ĵ���������P4���ڵ�A�ĶԳƵ�P5�����������
����һ�������ܴӵ�P1����ʼ���������ڵ�A��B��C��ѭ���Գ�����������һ��������P1���ڵ�A�ĶԳƵ�P2��������������P2���ڵ�B�ĶԳƵ�P3������������������P3���ڵ�C�ĶԳƵ�P4�������Ĵ���������P4���ڵ�A�ĶԳƵ�P5�����������![]() ������Ϊ________��
������Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�����A��3��0����B��4��1����һ�κ���y��kx+4��k��0��ͼ��ľ�����ȣ���k��ֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У�
��![]() ��
��
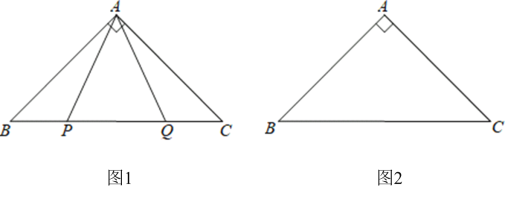
��1����ͼ1��![]() ��
��![]() �������㣬
�������㣬![]() �� ��
�� ��![]() �Ķ�����
�Ķ�����
��2����![]() ��
��![]() ����������(����
����������(����![]() �غ�)�� ��
�غ�)�� ��![]() �ڵ�
�ڵ�![]() ��࣬��
��࣬��![]() ����
����![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�Ϊ
�ĶԳƵ�Ϊ![]() ������
������![]() ��
��
�������⽫ͼ2��ȫ��
��С��ͨ���۲��ʵ�飬������룺�ڵ�![]() �˶��Ĺ����У�ʼ����
�˶��Ĺ����У�ʼ����![]() Ϊ����ֱ�������Σ��������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ�����֤�������˼·��Ҫ��֤��
Ϊ����ֱ�������Σ��������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ�����֤�������˼·��Ҫ��֤��![]() Ϊ����ֱ�������Σ�ֻ��֤
Ϊ����ֱ�������Σ�ֻ��֤![]() ��
��
��ο������˼·������С��֤����APM Ϊ����ֱ�������Σ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com