
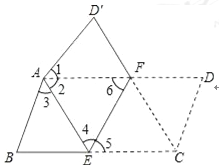
【题目】将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.

(1)求证:△ABE≌△AD′F;
(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.
【答案】见试题解析
【解析】试题分析:(1)根据平行四边形的性质及折叠的性质我们可以得到∠B=∠D′,AB=AD′,∠1=∠3,从而利用ASA判定△ABE≌△AD′F;
(2)四边形AECF是菱形,我们可以运用菱形的判定,有一组邻边相等的平行四边形是菱形来进行验证.
试题解析:(1)证明:由折叠可知:∠D=∠D′,CD=AD′,
∠C=∠D′AE.
∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD,∠C=∠BA D.
∴∠B=∠D′,AB=AD′,∠D′AE=∠BAD,
即∠1+∠2=∠2+∠3.
∴∠1=∠3.
又∠B=∠D′,AB=AD′
∴△ABE≌△AD′F(ASA).
(2)解:四边形AECF是菱形.
证明:由折叠可知:AE=EC,∠4=∠5.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠5=∠6.
∴∠4=∠6.
∴AF=AE.
∵AE=EC,
∴AF=EC.
又∵AF∥EC,
∴四边形AECF是平行四边形.
又∵AF=AE,
∴平行四边形AECF是菱形.


科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
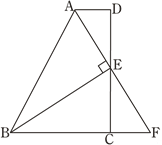
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F. 已知AD=2cm,BC=5cm.
(1)求证:FC=AD;
(2)求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个港口,水由A流向B,水流的速度是4千米/小时,甲、乙两船同时由A顺流驶向B,各自不停地在A、B之间往返航行,甲在静水中的速度是28千米/小时,乙在静水中的速度是20千米/小时.

设甲行驶的时间为t小时,甲船距B港口的距离为S1千米,乙船距B港口的距离为S2千米,如图为S1(千米)和t(小时)函数关系的部分图象.
(1)A、B两港口距离是_____千米.
(2)在图中画出乙船从出发到第一次返回A港口这段时间内,S2(千米)和t(小时)的函数关系的图象.
(3)求甲、乙两船第二次(不算开始时甲、乙在A处的那一次)相遇点M位于A、B港口的什么位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△CDE都是等边三角形,B,C,D三点在一条直线上,AD与BE交于点P,AC,BE交于点M,AD,CE交于点N,连接MN,则下列五个结论:①AD=BE;②∠BMC=∠ANE;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中一定正确的是__________.(填出所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角三角形的三边为边长向外作正方形,然后分别以三个正方形的中心为圆心,正方形边长的一半为半径作圆,记三个圆的面积分别为![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() 之间的关系是( )
之间的关系是( )

A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于![]() BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )
BC的长为半径作弧,两弧相交于点M、N;②作直线MN交AB于点D,连接CD,若CD=AD,∠B=20°,则下列结论中错误的是( )

A. ∠CAD=40° B. ∠ACD=70° C. 点D为△ABC的外心 D. ∠ACB=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年5月12日是我国第十个全国防灾减灾日,也是汶川地震十周年.为了弘扬防灾减灾文化,普及防灾减灾知识和技能,郑州W中学通过学校安全教育平台号召全校学生进行学习,并对学生学习成果进行了随机抽取,现对部分学生成绩(x为整数,满分100分)进行统计.绘制了如图尚不完整的统计图表:
调查结果统计表
组别 | 分数段 | 频数 |
A | 50≤x<60 | a |
B | 60≤x<70 | 80 |
C | 70≤x<80 | 100 |
D | 80≤x<90 | 150 |
E | 90≤x<100 | 120 |
合计 | b |
根据以上信息解答下列问题:
(1)填空:a= ,b= ;
(2)扇形统计图中,m的值为 ,“D”所对应的圆心角的度数是 度;
(3)本次调查测试成绩的中位数落在 组内;
(4)若参加学习的同学共有2000人,请你估计成绩在90分及以上的同学大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夷陵区园林处为了对一段公路进行绿化,计划购买A、B两种风景树,已知若用8000元买A种树要比买B种树多买20棵,A、B两种树的相关信息如下表:
项目品种 | 单价(元/棵) | 成活率 |
A | m | 91% |
B | 100 | 97% |
(1)求表中m的值;
(2)预计对这段公路的绿化需购1000棵这样的风景树.若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A、B两种树各多少棵?最低费用为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com