
【题目】如图,某校“综合实践”社团,计划利用![]() 长的栅栏材料,一边靠原有旧墙围成如图所示的两个矩形试验田,墙的长度为
长的栅栏材料,一边靠原有旧墙围成如图所示的两个矩形试验田,墙的长度为![]() .
.
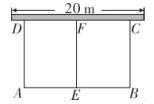
(1)能否围成总面积为![]() 的试验田?若能,求出
的试验田?若能,求出![]() 的长度;若不能,说明理由;
的长度;若不能,说明理由;
(2)能否围成总面积为![]() 的试验田?说说你的理由.
的试验田?说说你的理由.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】剪纸是中国传统的民间艺术,它画面精美,风格独特,深受大家喜爱,现有三张不透明的卡片,其中两张卡片的正面图案为“金鱼”,另外一张卡片的正面图案为“蝴蝶”,卡片除正面剪纸图案不同外,其余均相同.将这三张卡片背面向上洗匀从中随机抽取一张,记录图案后放回,重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法,求抽出的两张卡片上的图案都是“金鱼”的概率.(图案为“金鱼”的两张卡片分别记为A1、A2,图案为“蝴蝶”的卡片记为B)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 和反比例函数
和反比例函数![]() .
.
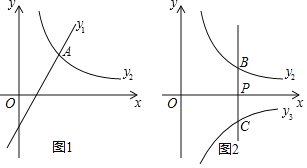
(1)如图1,若![]() ,且函数
,且函数![]() 、
、![]() 的图象都经过点
的图象都经过点![]() .
.
①求![]() ,
,![]() 的值;
的值;
②直接写出当![]() 时
时![]() 的范围;
的范围;
(2)如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 与函数
与函数![]() 的图象相交于点
的图象相交于点![]() ,与反比例函数
,与反比例函数![]() 的图象相交于点
的图象相交于点![]() .
.
①若![]() ,直线
,直线![]() 与函数
与函数![]() 的图象相交点
的图象相交点![]() .当点
.当点![]() 、
、![]() 、
、![]() 中的一点到另外两点的距离相等时,求
中的一点到另外两点的距离相等时,求![]() 的值;
的值;
②过点![]() 作
作![]() 轴的平行线与函数
轴的平行线与函数![]() 的图象相交于点
的图象相交于点![]() .当
.当![]() 的值取不大于1的任意实数时,点
的值取不大于1的任意实数时,点![]() 、
、![]() 间的距离与点
间的距离与点![]() 、
、![]() 间的距离之和
间的距离之和![]() 始终是一个定值.求此时
始终是一个定值.求此时![]() 的值及定值
的值及定值![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.
(1)等边三角形“內似线”的条数为 ;
(2)如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“內似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别在边AC、BC上,且EF是△ABC的“內似线”,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() ,过点
,过点![]() 和点
和点![]() ,与y轴交于点C,连接AC交x轴于点D,连接OA,OB
,与y轴交于点C,连接AC交x轴于点D,连接OA,OB
![]() 求抛物线
求抛物线![]() 的函数表达式;
的函数表达式;
![]() 求点D的坐标;
求点D的坐标;
![]() 的大小是______;
的大小是______;
![]() 将
将![]() 绕点O旋转,旋转后点C的对应点是点
绕点O旋转,旋转后点C的对应点是点![]() ,点D的对应点是点
,点D的对应点是点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点M,在
交于点M,在![]() 旋转过程中,当点M与点
旋转过程中,当点M与点![]() 重合时,请直接写出点M到AB的距离.
重合时,请直接写出点M到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
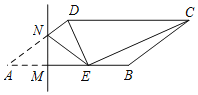
【题目】如图,已知ABCD中,AB=16,AD=10,sinA=![]() ,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
,点M为AB边上一动点,过点M作MN⊥AB,交AD边于点N,将∠A沿直线MN翻折,点A落在线段AB上的点E处,当△CDE为直角三角形时,AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
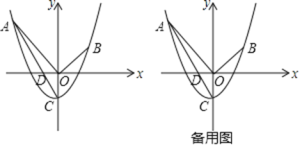
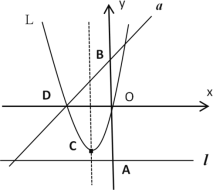
【题目】如图,若m是正数,直线l:y=-m与y轴交于点A;直线a:y=x+m与y轴交于点B;抛物线L:y= x2+mx的顶点为C,且L与x轴左交点为D.
(1)若AB=12,求m的值,此时在抛物线的对称轴上存在一点P使得△![]() 的周长最小,求点P坐标;
的周长最小,求点P坐标;
(2)当点C在直线l上方时,求点C与直线l距离的最大值;
(3)在抛物线L和直线a所围成的封闭图形的边界上,把横、纵坐标都是整数的点称为“美点”,分别直接写出m=2020和m=2020.5时“美点”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
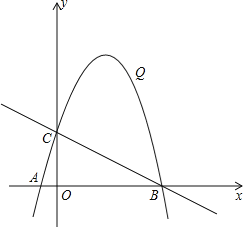
(1)求出△ABC的周长.
(2)在直线BC上方有一点Q,连接QC、QB,当△QBC面积最大时,一动点P从Q出发,沿适当路径到达y轴上的M点,再沿与对称轴垂直的方向到达对称轴上的N点,连接BN,求QM+MN+BN的最小值.
(3)在直线BC上找点G,K是平面内一点,在平面内是否存在点G,使以O、C、G、K为顶点的四边形是菱形?若存在,求出K的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com