
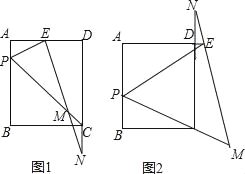
【题目】如图1,矩形ABCD中,P是AB边上的一点(不与A,B重合),PE平分∠APC交射线AD于E,过E作EM⊥PE交直线CP于M,交直线CD于N.
(1)求证:CM=CN;
(2)若AB:BC=4:3,
①当![]() = 时,E恰好是AD的中点;
= 时,E恰好是AD的中点;
②如图2,当△PEM与△PBC相似时,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() .
.
【解析】试题分析:(1)由矩形的性质得出∠A=∠ADC=90°,AB=CD,AD=BC,由平行线的性质、互余两角关系、对顶角相等以及角平分线证出∠CMN=∠N,即可得出结论;
(2)①由题意得出M、N、C三点重合,由ASA证明△APE≌△DFE,得出AP=DF,PE=FE,由线段垂直平分线的性质证出AP+CD=PC,设AD=3,AB=4,过P作PF⊥CD于F,设AP=DE=x,则PB=CF=4﹣x,PC=4+x,PF=3,由勾股定理得出方程,解方程即可;
②分两种情况:1.若△PEM∽△CCBP,则∠EPM=∠BCP,得出PE∥BC,不成立;
2.若△PEM∽△PBC,则∠APB=∠EPM=∠BPC=60°,设AB=4a,BC=AD=3a,则PB=![]() a,AP=(
a,AP=(![]() )a,AE=(
)a,AE=(![]() )a,设PE与CD交于点F,证出△PEM∽△FEN,由相似三角形的性质和平行线分线段成比例定理得出
)a,设PE与CD交于点F,证出△PEM∽△FEN,由相似三角形的性质和平行线分线段成比例定理得出![]() ,即可得出结果.
,即可得出结果.
试题解析:解:(1)延长PE交CD的延长线于F,如图1所示:
∵四边形ABCD是矩形,∴AB∥CD,∠A=∠ADC=∠EDF═90°,AB=CD,AD=BC,∴∠APE+∠AEP=90°,∴∠F=∠APE,∵EM⊥EN,∴∠PEN=∠FEN=90°,∴∠CPE+∠PME=90°,∠F+∠N=90°,∵PE平分∠APC,∴∠APE=∠MPE,又∵∠PME=∠CMN,∴∠CMN=∠N,∴CM=CN;
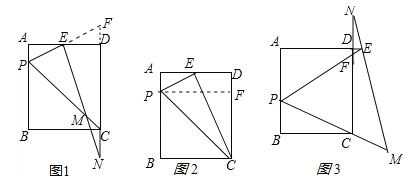
(2)①若E是AD的中点,则M、N、C三点重合,∵E为AD的中点,∴AE=DE,在△APE和△DFE中,∵∠A=∠EDF,AE=DE,∠AEP=∠DEF,∴△APE≌△DFE(ASA),∴AP=DF,PE=FE,∵EM⊥EN,∴PC=FC,∵FC=CD+DF,∴AP+CD=PC,设AD=3a,AB=4a,过P作PF⊥CD于F,如图2所示:
设AP=DE=x,则PB=CF=4﹣x,PC=4+x,PF=3,由勾股定理得:(4﹣x)2+32=(4+x)2,解得:x=![]() a,4﹣x=
a,4﹣x=![]() a,∴
a,∴![]() =
=![]() ;
;
②分两种情况:
1.若△PEM∽△CCBP,则∠EPM=∠BCP,∴PE∥BC,不成立;
2.若△PEM∽△PBC,则∠APE=∠EPM=∠BPC=60°,设AB=4a,BC=AD=3a,则PB=![]() a,AP=(
a,AP=(![]() )a,AE=(
)a,AE=(![]() )a,设PE与CD交于点F,如图3所示:
)a,设PE与CD交于点F,如图3所示:
∵AB∥CD,∴∠EFN=∠BFC=∠APE=60°,∴∠N=∠M=90°﹣60°=30°,∵EM⊥PE,∴∠NEF=∠PEM=90°,∴△PEM∽△FEN,∴ ![]() ,∵AB∥CD,∴
,∵AB∥CD,∴![]() ,∴
,∴![]() =
=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一幅长为80cm,宽为50cm的矩形风景画的四周镶一条相同宽度的边框,制成一幅挂图,如图所示,设边框的宽为xcm,如果整个挂图的面积是5400cm2 ,那么下列方程符合题意的是( )
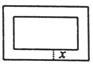
A. (50-x)(80-x)=5400 B. (50-2x)(80-2x)=5400
C. (50+x)(80+x)=5400 D. (50+2x)(80+2x)=5400
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O.
(1)求证:OB=OC;
(2)若∠ABC=55°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是8m,宽是2m,抛物线的最高点到路面的距离为6米.
(1)按如图所示建立平面直角坐标系,求表示该抛物线的函数表达式;
(2)一辆货运卡车高为4m,宽为2m,如果该隧道内设双向车道,那么这辆货车能否安全通过?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E,
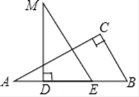
(1)试说明△ABC与△MED全等;
(2)若∠M=35°,求∠B的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】因魔幻等与众不同的城市特质,以及抖音等新媒体的传播,重庆已成为国内外游客最喜欢的旅游目的地城市之一.著名“网红打卡地”磁器口在2018年五一长假期间,接待游客达20万人次,预计在2020年五一长假期间,接待游客将达28.8万人次.在磁器口老街,美食无数,一家特色小面店希望在五一长假期间获得好的收益,经测算知,该小面成本价为每碗6元,借鉴以往经验:若每碗卖25元,平均每天将销售300碗,若价格每降低1元,则平均每天多销售30碗.
(1)求出2018至2020年五一长假期间游客人次的年平均增长率;
(2)为了更好地维护重庆城市形象,店家规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天利润6300元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全年级学生英语作业的完成情况,帮助英语学习成绩差的学生尽快提高成绩,班主任和英语教师从全年级![]() 名学生中抽取
名学生中抽取![]() 名进行调查.首先,老师检查了这些学生的作业本,记录下获得“优”、“良”、“中”、“差”的人数比例情况;其次老师发给每人一张调查问卷,其中有一个调查问题是:“你的英语作业完成情况如何?”,给出五个选项:A.独立完成;B.辅导完成;C.有时抄袭完成;D.经常抄袭完成;E.经常不完成,供学生选择,英语教师发现选独立完成和辅导完成这两项的学生一共占
名进行调查.首先,老师检查了这些学生的作业本,记录下获得“优”、“良”、“中”、“差”的人数比例情况;其次老师发给每人一张调查问卷,其中有一个调查问题是:“你的英语作业完成情况如何?”,给出五个选项:A.独立完成;B.辅导完成;C.有时抄袭完成;D.经常抄袭完成;E.经常不完成,供学生选择,英语教师发现选独立完成和辅导完成这两项的学生一共占![]() ,明显高于他平时观察到的比例,请回答下列问题:
,明显高于他平时观察到的比例,请回答下列问题:
(1)英语教师所用的调查方式是_______;
(2)如果老师的英语作业检查只得“差”的同学有![]() 名,那么估计全年级的英语作业中可能有多少同学得“差”;
名,那么估计全年级的英语作业中可能有多少同学得“差”;
(3)通过问卷调查,老师得到的数据与事实不符,请你解释这个统计数字失真的原因.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com