
�ס��������̳�������ͬ��ij����Ʒ��ÿ���ۼ۾�Ϊ3000Ԫ�����Ҷ�����һ�����Żݣ����̳����Ż������ǣ���һ����ԭ�ۼ��շѣ�����ÿ���Ż�30%�����̳����Ż������ǣ�ÿ���Ż�25%����������ƷΪx��ʱ�����̳��շ�Ϊy1Ԫ�����̳��շ�Ϊy2Ԫ��
��1���ֱ����y1��y2��x֮��Ĺ�ϵʽ��
��2�����ס��������̳����շ���ͬʱ��������ƷΪ���ټ���
��3����������ƷΪ5��ʱ��Ӧѡ���ĸ��̳����Żݣ���˵�����ɣ�
��1�� ��y2=2250x��
��y2=2250x��
��2���ס��������̳����շ���ͬʱ��������ƷΪ6����
��3��������ƷΪ5��ʱ��Ӧѡ�����̳����Żݣ�
���������������1���������̳����Żݷ����ֱ���ʽ�������ɣ�
��2�����շ���ͬ���г�������⼴�ɣ�
��3���ɺ�������ʽ�ֱ����x=5ʱ�ĺ���ֵ�����ɵý�
�����������1����x=1ʱ��y1=3000��
��x��1ʱ��y1=3000+3000��x��1������1��30%��=2100x+900��
�� ��
��
y2=3000x��1��25%��=2250x��
��y2=2250x��
��2�����ס��������̳����շ���ͬʱ��2100x+900=2250x��
���x=6��
�𣺼ס��������̳����շ���ͬʱ��������ƷΪ6����
��3��x=5ʱ��y1=2100x+900=2100��5+900=11400��
y2=2250x=2250��5=11250��
��11400��11250��
��������ƷΪ5��ʱ��Ӧѡ�����̳����Żݣ�
���㣺һ�κ�����Ӧ�á�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У�������OABC�ı߳�Ϊa��ֱ��y=bx+c��x����E����y����F����a��b��c�ֱ�����-(a-4)2��0��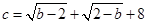
��1����ֱ��y=bx+c�Ľ���ʽ��ֱ��д��������OABC�ĶԽ��ߵĽ���D�����ꣻ
��2��ֱ��y=bx+c��x����������ÿ���ƶ�1����λ���ȵ��ٶ�ƽ�ƣ���ƽ�Ƶ�ʱ��Ϊt�룬���Ƿ����t��ֵ��ʹֱ��EFƽ��������OABC������������ڣ������t��ֵ���������ڣ���˵�����ɣ�
��PΪ������OABC�ĶԽ���AC�ϵĶ��㣨�˵�A��C���⣩��PM��PO����ֱ��AB��M���� ��ֵ
��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��ֱ��y=x+b��b��0������������A��B���㣬��D��ֱ���ϣ�D�ĺ�������֮��Ϊ2����D����������Ĵ���DC��DE������OD��
��1����֤��ADƽ�֡�CDE��
��2���������ʵ��b��b��0������֤��AD•BDΪ��ֵ��
��3���Ƿ����ֱ��AB��ʹ���ı���OBCDΪƽ���ı��Σ������ڣ����ֱ�ߵĽ���ʽ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪һ�κ���ͼ����ͼ��
��1����һ�κ����Ľ���ʽ��
��2������PΪ��һ�κ���ͼ����һ�㣬�ҵ�AΪ�ú���ͼ����x��Ľ��㣬��S��PAO=6�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��һ������ȼ��ʵ���У�����ȼ��ʱʣ�ಿ�ֵĸ߶�y��cm����ȼ��ʱ��x��h��֮��Ϊһ�κ�����ϵ������ͼ���ṩ����Ϣ������������⣺
��1���������ȼ��ʱy��x֮��ĺ�����ϵʽ��
��2��������ӵ�ȼ��ȼ�����õ�ʱ�䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��һ����ֱ�Ĺ�·��������A��B��C������ׯ���ס�������ͬʱ�ֱ��A��B�������������Ħ�г�������綯���ع�·����ʻ��C�壬���յ���C�壮��ס������˵�C��ľ���y1��y2��km������ʻʱ��x��h��֮��ĺ�����ϵ��ͼ��ʾ����ش��������⣺
��1��A��C�����ľ���Ϊ�� ��km��a=�� ����
��2�����ͼ�е�P�����꣬�����õ���������ʾ��ʵ�����壻
��3��������ʻ�����У���ʱ���10km��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ƽ��ֱ������ϵ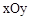 �У�һ�κ���
�У�һ�κ��� ��aΪ��������ͼ����y���ཻ�ڵ�A���뺯��
��aΪ��������ͼ����y���ཻ�ڵ�A���뺯�� ��ͼ���ཻ�ڵ�B
��ͼ���ཻ�ڵ�B ��
�� ��
��
��1�����B�����꼰һ�κ����Ľ���ʽ��
��2������P��y���ϣ��ҡ�PABΪֱ�������Σ���ֱ��д����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ƽ��ֱ������ϵ �У�һ�κ���
�У�һ�κ��� �ͷ���������
�ͷ��������� ��ͼ������
��ͼ������ .
.
��1���� ��ֵ��һ�κ����ı���ʽ��
��ֵ��һ�κ����ı���ʽ��
��2����B��˫���� �ϣ���λ��ֱ��
�ϣ���λ��ֱ�� ���·�������B�ĺᡢ�����궼��������ֱ��д����B������.
���·�������B�ĺᡢ�����궼��������ֱ��д����B������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�� ��
�� ��������������ʵ�������ǹ涨�����㲻��ʽ
��������������ʵ�������ǹ涨�����㲻��ʽ ��
�� ��
�� ��ʵ��
��ʵ�� ������ȡֵ��ȫ����������䣬��ʾΪ
������ȡֵ��ȫ����������䣬��ʾΪ . ����һ����������������Ա���
. ����һ����������������Ա��� �뺯��ֵ
�뺯��ֵ ���㣺��m��
���㣺��m�� ��nʱ����m��
��nʱ����m�� ��n�����Ǿͳƴ˺����DZ�����
��n�����Ǿͳƴ˺����DZ����� �ϵġ��պ�����.
�ϵġ��պ�����.
��1������������ �DZ�����
�DZ����� �ϵġ��պ����������жϲ�˵�����ɣ�
�ϵġ��պ����������жϲ�˵�����ɣ�
��2����һ�κ���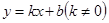 �DZ�����
�DZ����� �ϵġ��պ���������˺����ı���ʽ��
�ϵġ��պ���������˺����ı���ʽ��
��3��������� �DZ�����
�DZ����� �ϵġ��պ�������ֱ��д��ʵ��
�ϵġ��պ�������ֱ��д��ʵ�� ��
�� ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com