
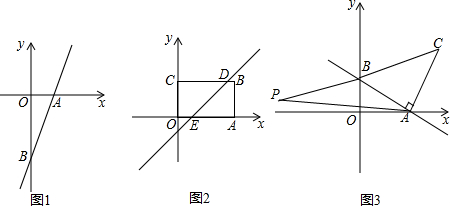
���� ��1�������A��B�����꣬�ó�OA=3��OB=6����S��ABC=2S��AOB ���ó�AC=2OA=6���ٵ���C�ڵ�A���ұ�ʱ���ó�OC�����ɵó���C���ꣻ
�ڵ���C�ڵ�A�����ʱ�����OC�����ɵó���C���ꣻ
��2����ֱ�߽���ʽ�ó�E��$\frac{2}{k}$��0����D��$\frac{8}{k}$��0����������ó�����OEDC�����=$\frac{1}{2}$��$\frac{2}{k}+\frac{8}{k}$����6=$\frac{1}{2}$��15��6���������k��
��3������P��AB��ƽ���ߣ���CA���ӳ�����D����x����M����PE��AB��E����֤���ı���ADPE�Ǿ��Σ��ó�AD=PE�����A��B�����꣬�ó�OA��OB���ɹ��ɶ������AB�������ABC��������ɡ�ABP��������ABC�������ȣ����PE���ó�AD��AM��OM�����M�����꣬�����ֱ��PD�Ľ���ʽ���ѵ�P��a��$\frac{1}{2}$�����룬�������aֵ��
��� �⣺��1����y=2x-6����y=0ʱ��x=3����x=0ʱ��y=-6��
��A��3��0����B��0��-6����
��OA=3��OB=6��
��S��ABC=2S��AOB ��
��$\frac{1}{2}$AC•OB=2��$\frac{1}{2}$��OA•OB��
��AC=2OA=6��
�ٵ���C�ڵ�A���ұ�ʱ��OC=3+6=9��
��C��9��0����
�ڵ���C�ڵ�A�����ʱ��OC=6-3=3��
��C��-3��0����
������������C����������9��0������-3��0����
��2����y=kx-2����y=0ʱ��x=$\frac{2}{k}$����y=6ʱ��x=$\frac{8}{k}$��
��E��$\frac{2}{k}$��0����D��$\frac{8}{k}$��0����
��ֱ��y=kx-2ǡ�ý�����OABC��Ϊ�����ȵ������֣�
������OEDC�����=$\frac{1}{2}$��$\frac{2}{k}+\frac{8}{k}$����6=$\frac{1}{2}$��15��6��
��ã�k=$\frac{2}{3}$��
��3������P��AB��ƽ���ߣ���CA���ӳ�����D����x����M����PE��AB��E����ͼ��ʾ��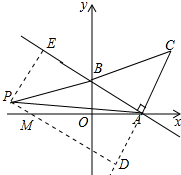 ���AMD=��BAO��PE��AD��
���AMD=��BAO��PE��AD��
���ı���ADPE�Ǿ��Σ�
��AD=PE��
��ֱ��y=-$\frac{\sqrt{3}}{3}$x+1��x�ᡢy��ֱ��ཻ�ڵ�A��B����y=0ʱ��x=$\sqrt{3}$����x=0ʱ��y=1��
��A��$\sqrt{3}$��0����B��0��1����
��OA=$\sqrt{3}$��OB=1��
��AB=$\sqrt{��\sqrt{3}��^{2}+{1}^{2}}$=2����BAO=30�㣬
���AMD=30�㣬
�ߡ�ABC�ǵ���ֱ�������Σ���BAC=90�㣬
��AC=AB=2��
���ABC�����=$\frac{1}{2}$��2��2=2��
�ߡ�ABP��������ABC�������ȣ�
���ABP�����=$\frac{1}{2}$AB•PE=$\frac{1}{2}$��2��PE=2��
��PE=2��
��AD=2����AM=2AD=4��
��OM=4-$\sqrt{3}$��
��M��$\sqrt{3}$-4��0����
��ֱ��PD�Ľ���ʽΪy=-$\frac{\sqrt{3}}{3}$x+b��
�ѵ�M��$\sqrt{3}$-4��0������ã�b=1-$\frac{4\sqrt{3}}{3}$��
��ֱ��PD�Ľ���ʽΪy=-$\frac{\sqrt{3}}{3}$x+1-$\frac{4\sqrt{3}}{3}$��
�ѵ�P��a��$\frac{1}{2}$������ã�a=-4+$\frac{\sqrt{3}}{2}$��
���� ������һ�κ����ۺ���Ŀ��������ͼ�����������ʡ�һ�κ�������ʽ�������ε��ж������ʡ����ɶ���������ֱ�������ε����ʡ������κ���������ļ����֪ʶ�������ѶȽϴ��ۺ���ǿ����1���У���Ҫ���з������ۣ��ر��ǣ�3���У���Ҫͨ���������ߣ����������ϵȷ����������һ�κ�������ʽ���ܵó������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{25}$=��5 | B�� | ��$\sqrt{25}$=5 | C�� | $\sqrt{{��{-5}��}^2}$=5 | D�� | $\sqrt{{��{-3}��}^2}$=-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
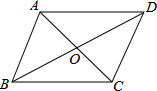 ��ͼ��ƽ���ı���ABCD�ĶԽ����ཻ�ڵ�O����������һ������AC=BD���𰸲�Ψһ������ֻ��һ�����ɣ���ʹƽ���ı���ABCD�Ǿ��Σ�
��ͼ��ƽ���ı���ABCD�ĶԽ����ཻ�ڵ�O����������һ������AC=BD���𰸲�Ψһ������ֻ��һ�����ɣ���ʹƽ���ı���ABCD�Ǿ��Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
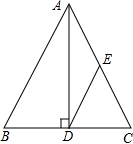 ��ͼ���ڡ�ABC�У�AB=AC��AD��BC������ΪD��E��AC�е㣬��DE=2����AB�ij�Ϊ4��
��ͼ���ڡ�ABC�У�AB=AC��AD��BC������ΪD��E��AC�е㣬��DE=2����AB�ij�Ϊ4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
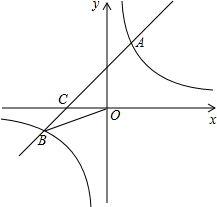 ��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��ͼ���뷴��������y=$\frac{k}{x}$��ͼ����һ���������ڵ�A��B���㣬��x�ύ��C�㣬��A������Ϊ��2��m������B������Ϊ��n��-2����tan��BOC=$\frac{1}{2}$��
��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=ax+b��ͼ���뷴��������y=$\frac{k}{x}$��ͼ����һ���������ڵ�A��B���㣬��x�ύ��C�㣬��A������Ϊ��2��m������B������Ϊ��n��-2����tan��BOC=$\frac{1}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 8 | C�� | 10 | D�� | 17 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������A B������AC��ɵĽ��ּܣ�����AB=AC=5�ף��Ϧ�=70�㣮
��ͼ��������A B������AC��ɵĽ��ּܣ�����AB=AC=5�ף��Ϧ�=70�㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com