
【题目】如图,在平面直角坐标系中,一直线![]() 分别于
分别于![]() 轴、
轴、![]() 轴交于A、B两点,点A、点D关于原点对称,过点A的抛物线
轴交于A、B两点,点A、点D关于原点对称,过点A的抛物线![]() 与射线AB交于另一点C,若将
与射线AB交于另一点C,若将![]() 沿着CO所在的直线翻折得到
沿着CO所在的直线翻折得到![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() 的
的![]() .
.
(1)求B、D两点的坐标(用m的代数式表示).
(2)当![]() 落在抛物线上时,求二次函数的解析式.
落在抛物线上时,求二次函数的解析式.

【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)根据直线上点的特点直接求解;
(2)由面积关系,判断E是CD中点,OE是△ACD中位线,直线CA′与抛物线有两个交点,利用韦达定理,求出q=3m2,进而求出A点坐标,求解m;
(1)直线y=![]() x+
x+![]() m(m>0)分别于x轴、y轴交于A、B两点,
m(m>0)分别于x轴、y轴交于A、B两点,
∴A(-5m,0),B(0,![]() m),D(5m,0),
m),D(5m,0),
(2)∵△A′CO与△COD重叠部分的面积为△COD的![]() .
.
∴M是CD的中点,
又∵O是AD中点,
∴OE∥AC,OE=![]() AC=
AC=![]() CA′,
CA′,
∴∠DOE=∠OAC=∠A′,
∴CA′∥AD,A′C=OA=5m,
设A′(p,q),C、A′的横坐标分别是xC、xA′,
-![]() x2+
x2+![]() mx+
mx+![]() m2=q,
m2=q,
∴xC+xA′=3m,xCxA′=12q-40m2,
(xC-xA′)2=(xC+xA′)2-4xCxA′,
(5m)2=(3m)2-4(12q-40m2),
∴q=3m2,
∴A(4m,3m2)
∴(4m)2+(3m2)2=(5m)2,
∴m=1,
∴函数解析式为y=--![]() x2+
x2+![]() mx+
mx+![]() ,
,



 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
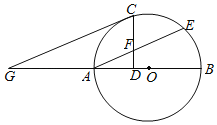
【题目】如图所示,AB是⊙O的直径,AE是弦,C是劣弧AE的中点,过C作CD⊥AB于点D,CD交AE于点F,过C作CG∥AE交BA的延长线于点G.
(1)求证:CG是⊙O的切线.
(2)求证:AF=CF.
(3)若sinG=0.6,CF=4,求GA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
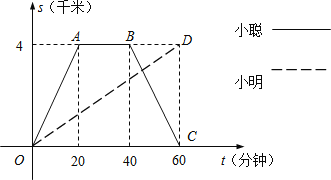
【题目】小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料,学校与图书馆的路程是4千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线O-A-B-C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在图书馆查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟;
(2)请你求出小明离开学校的路程s(千米)与所经过的时间t(分钟)之间的函数表达式;
(3)若设两人在路上相距不超过0.4千米时称为可以“互相望见”,则小聪和小明可以“互相望见”的时间共有多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
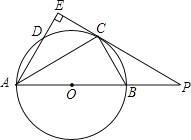
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC.
(1)求证:AC平分∠BAD;
(2)若AB=3,AC=2![]() ,求EC和PB的长.
,求EC和PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
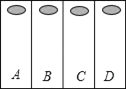
【题目】如图是某教室里日光灯的四个控制开关(分别记为A、B、C、D),每个开关分别控制一排日光灯(开关序号与日光灯的排数序号不一定一致).某天上课时,王老师在完全不知道哪个开关对应控制哪排日光灯的情况下先后随机按下两个开关.
(1)求王老师按下第一个开关恰好能打开第一排日光灯的概率;
(2)王老师按下两个开关恰好能打开第一排与第三排日光灯的概率是多少?请列表格或画树状图加以分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
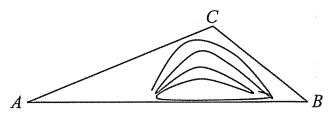
【题目】修建隧道可以方便出行.如图:![]() ,
,![]() 两地被大山阻隔,由
两地被大山阻隔,由![]() 地到
地到![]() 地需要爬坡到山顶
地需要爬坡到山顶![]() 地,再下坡到
地,再下坡到![]() 地.若打通穿山隧道,建成直达
地.若打通穿山隧道,建成直达![]() ,
,![]() 两地的公路,可以缩短从
两地的公路,可以缩短从![]() 地到
地到![]() 地的路程.已知:从
地的路程.已知:从![]() 到
到![]() 坡面的坡度
坡面的坡度![]() ,从
,从![]() 到
到![]() 坡面的坡角
坡面的坡角![]() ,
,![]() 公里.
公里.
(1)求隧道打通后从![]() 到
到![]() 的总路程是多少公里?(结果保留根号)
的总路程是多少公里?(结果保留根号)
(2)求隧道打通后与打通前相比,从![]() 地到
地到![]() 地的路程约缩短多少公里?(结果精确到0.01)(
地的路程约缩短多少公里?(结果精确到0.01)(![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
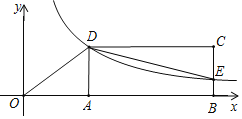
【题目】如图,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数y=![]() 在第一象限内的图象与直线y=
在第一象限内的图象与直线y=![]() x交于点D,且反比例函数y=
x交于点D,且反比例函数y=![]() 交BC于点E,AD=3.
交BC于点E,AD=3.
(1)求D点的坐标及反比例函数的关系式;
(2)若矩形的面积是24,请写出△CDE的面积(不需要写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“重整行装再出发,驰而不息再争创”,2018年5月8日兰州市召开了新一轮全国文明城市创建启动大会.某校为了更好地贯彻落实创建全国文明城市目标,举办了“我是创城小主人”的知识竞赛.该校七年级、八年级分别有300人,现从中各随机抽取10名同学的测试成绩进行调查分析,成绩如下:
七年级 | 85 | 65 | 84 | 78 | 100 | 78 | 85 | 85 | 98 | 83 |
八年级 | 96 | 60 | 87 | 78 | 87 | 87 | 89 | 100 | 83 | 96 |
整理、描述数据:
分数段 |
|
|
|
|
七年级人数 | 1 | 2 | 5 | 2 |
八年级人数 | 1 | 1 | 5 | 3 |
分析数据:
年级 | 平均数 | 中位数 | 众数 |
七 | 84.1 | _______ | 85 |
八 | 86.3 | 87 | ______ |
得出结论:
(1)根据上述数据,将表格补充完整;
(2)估计该校七、八两个年级学生在本次测试成绩中可以取得优秀的人数![]() 共有多少人?
共有多少人?
(3)你认为哪个年级知识掌握的总体水平较好,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
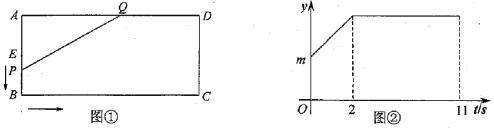
【题目】如图①,在矩形![]() 中,点
中,点![]() 从
从![]() 边的中点
边的中点![]() 出发,沿着
出发,沿着![]() 速运动,速度为每秒2个单位长度,到达点
速运动,速度为每秒2个单位长度,到达点![]() 后停止运动,点
后停止运动,点![]() 是
是![]() 上的点,
上的点,![]() ,设
,设![]() 的面积为
的面积为![]() ,点
,点![]() 运动的时间为
运动的时间为![]() 秒,
秒,![]() 与
与![]() 的函数关系如图②所示.
的函数关系如图②所示.
(1)图①中![]() = ,
= ,![]() = ,图②中
= ,图②中![]() = .
= .
(2)当![]() =1秒时,试判断以
=1秒时,试判断以![]() 为直径的圆是否与
为直径的圆是否与![]() 边相切?请说明理由:
边相切?请说明理由:
(3)点![]() 在运动过程中,将矩形沿
在运动过程中,将矩形沿![]() 所在直线折叠,则
所在直线折叠,则![]() 为何值时,折叠后顶点
为何值时,折叠后顶点![]() 的对应点
的对应点![]() 落在矩形的一边上.
落在矩形的一边上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com