
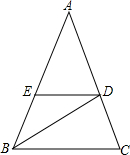
 在△ABC中,∠ABC=∠C=2∠A,BD是∠ABC的平分线,DE∥BC,则图中等腰三角形的个数是( )
在△ABC中,∠ABC=∠C=2∠A,BD是∠ABC的平分线,DE∥BC,则图中等腰三角形的个数是( )| A、5 | B、4 | C、3 | D、2 |


科目:初中数学 来源: 题型:
 定义:如果二次函数y=ax2+bx+c的最小值大于0,我们就说这个二次函数的值恒大于0.
定义:如果二次函数y=ax2+bx+c的最小值大于0,我们就说这个二次函数的值恒大于0.查看答案和解析>>
科目:初中数学 来源: 题型:
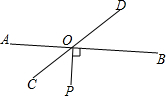 如图所示,草原上有两条交叉的河流AB,CD,有一个牧民在点P处放牧,且OP⊥AB于点O,理论上若他欲使羊群喝水的路程最短,他应作何选择?请你画出图形说明.
如图所示,草原上有两条交叉的河流AB,CD,有一个牧民在点P处放牧,且OP⊥AB于点O,理论上若他欲使羊群喝水的路程最短,他应作何选择?请你画出图形说明.查看答案和解析>>
科目:初中数学 来源: 题型:
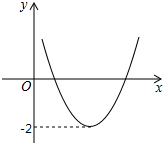 二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有四个实数根,则k的取值范围是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有四个实数根,则k的取值范围是( )| A、k<2 | B、k>2 |
| C、0<k<2 | D、-2<k<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.
如图,在Rt△ABC中,∠ABC=90°,CD⊥BC,BD与AC相交于点E,AB=9,BC=4,DC=3.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com