
 如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,以B为圆心,BA为半径画弧交CB的延长线于点D,则$\widehat{AD}$的长为$\frac{4π}{3}$.
如图,在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,以B为圆心,BA为半径画弧交CB的延长线于点D,则$\widehat{AD}$的长为$\frac{4π}{3}$. 分析 先解Rt△ABC,根据30°角所对的直角边等于斜边的一半得出AB=2BC=2,求出∠ABC=60°,那么∠ABD=120°,再根据弧长的计算公式即可求解.
解答 解:∵在Rt△ABC中,∠C=90°,∠BAC=30°,BC=1,
∴AB=2BC=2,∠ABC=90°-∠BAC=60°,
∴∠ABD=180°-∠ABC=120°,
∴$\widehat{AD}$=$\frac{120×π×2}{180}$=$\frac{4π}{3}$.
故答案为$\frac{4π}{3}$.
点评 本题考查了弧长的计算公式:l=$\frac{nπR}{180}$(弧长为l,圆心角度数为n,圆的半径为R),也考查了解直角三角形,求出AB的长与∠ABD的度数是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | BC=BA,B′C′=B′A′,∠B=∠B′ | B. | ∠A=∠B′,AC=A′B′,AB=B′C′ | ||
| C. | ∠A=∠A′,AB=B′C′,AC=A′C′ | D. | BC=B′C′,AC=A′B′,∠B=∠C′ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>-$\frac{a}{2}$ | B. | x>-$\frac{a}{3}$ | C. | x>$\frac{a}{3}$ | D. | x>$\frac{a}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4.
如图,已知函数y=2x和函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 根据“边边边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| B. | 根据“边角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| C. | 根据“角边角”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB | |
| D. | 根据“角角边”可知,△C′O′D′≌△COD,所以∠A′O′B′=∠AOB |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
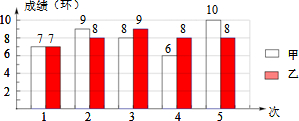
| A. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2=S_乙^2$ | B. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2>S_乙^2$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,$S_甲^2<S_乙^2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某实践小组去公园测量人工湖AD的长度.小明进行如下测量:点D在点A的正北方向,点B在点A的北偏东50°方向,AB=40米.点E在点B的正北方向,点C在点B的北偏东30°方向,CE=30米.点C和点E都在点D的正东方向,求AD的长(结果精确到1米).(参考数据:$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
某实践小组去公园测量人工湖AD的长度.小明进行如下测量:点D在点A的正北方向,点B在点A的北偏东50°方向,AB=40米.点E在点B的正北方向,点C在点B的北偏东30°方向,CE=30米.点C和点E都在点D的正东方向,求AD的长(结果精确到1米).(参考数据:$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com