
| 1 |
| x |
| 1 |
| x |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| 10 |
| 3 |
| 1 |
| 3 |
| 1 |
| x |
| 26 |
| 5 |
| 1 |
| x |
| 1 |
| a |
| 1 |
| x |
| 26 |
| 5 |
| 1 |
| 5 |
| a2+1 |
| a |
| 1 |
| a |
| 26 |
| 5 |
| 26 |
| 5 |
| 13 |
| 5 |
| 13 |
| 5 |
| 13 |
| 5 |
| 144 |
| 25 |
| 13 |
| 5 |
| 12 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| 10 |
| 3 |
| 1 |
| 3 |
| 1 |
| x |
| 26 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| x |
| a2+1 |
| a |
| a2+1 |
| a |
| 1 |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列方程及其解的特征:
(1)![]() 的解为
的解为![]() ; (2)
; (2)![]() 的解为
的解为![]() ;
;
(3)![]() 的解为
的解为![]() ; …… ……
; …… ……
解答下列问题
1.请猜想:方程![]() 的解为 ;
的解为 ;
2.请猜想:关于![]() 的方程
的方程![]() 的解为
的解为![]() ;(3)下面以解方程
;(3)下面以解方程![]() 为例,验证(1)中猜想结论的正确性
为例,验证(1)中猜想结论的正确性
查看答案和解析>>
科目:初中数学 来源:2011年汕头市九年级第一学期期末考试数学卷 题型:解答题
观察下列方程及其解的特征:
(1) 的解为
的解为 ; (2)
; (2) 的解为
的解为 ;
;
(3) 的解为
的解为 ; …… ……
; …… ……
解答下列问题:
【小题1】请猜想:方程 的解为 ;
的解为 ;
【小题2】请猜想:关于 的方程
的方程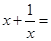 的解为
的解为 ;
;
【小题3】下面以解方程 为例,验证(1)中猜想结论的正确性.
为例,验证(1)中猜想结论的正确性.
解:原方程可化为 .(下面请大家用配方法写出解此方程的详细过程)
.(下面请大家用配方法写出解此方程的详细过程)
查看答案和解析>>
科目:初中数学 来源:2011年汕头市九年级第一学期期末考试数学卷 题型:解答题
观察下列方程及其解的特征:
(1) 的解为
的解为 ;
(2)
;
(2) 的解为
的解为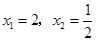 ;
;
(3) 的解为
的解为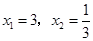 ; ……
……
; ……
……
解答下列问题:
1.请猜想:方程 的解为 ;
的解为 ;
2.请猜想:关于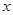 的方程
的方程 的解为
的解为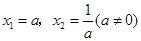 ;
;
3.下面以解方程 为例,验证(1)中猜想结论的正确性.
为例,验证(1)中猜想结论的正确性.
解:原方程可化为 .(下面请大家用配方法写出解此方程的详细过程)
.(下面请大家用配方法写出解此方程的详细过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com