练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    　　如图，在线段AB的同侧有等边△ACD和等边△CBE，且AE,BD相交于H，试问：

    （1）△ACE与△DCB能全等吗？试说明理由？

    （2）△ADH与△BDA能相似吗？试说明理由？

     

    答案：
    解析：

    		答案；(1) △ACE≌△DCB.理由: ∵DC=AC,CB=CE,∴∠ACE=∠DCB=120,故△ACE≌△DCB (2)由 (1)可知∠AEC=∠DBC, 又∠ECB=∠DAC=60.故CE∥AD,C从而∠AEC=∠DAH,因此∠DAH=∠DBA, 又∠ADH=∠BDA所以，△ADH∽△BDA

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：数学教研室 题型：013

    　　 如下图，在线段BC上取两点D、E，在线段BC外取一点A，连结AB、AD、AE、AC，则图中共有线段

    A.5条　　　　　　　　　　　　  B.8条　　　　　　　　　　　　  C.10条　　　　　　　　　　    D.12条

    　　 

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，Rt△ABC的斜边AB在x轴上，顶点C在y轴的负半轴上，tan∠ABC=，点P在线段OC上，且PO、PC的长(PO＜PC)是方程x2-12x+27=0的两根.

    　　(1)求P点坐标；

    　　(2)求AP的长；

    (3)在x轴上是否存在点Q，使以点A、C、P、Q为顶点的四边形是梯形？若存在，请直接写出直线PQ的解析式；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年广西省灌阳县七年级上学期期末质量检测数学卷 题型：填空题

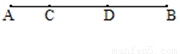
    如图，在线段AB上有两点C、D，AB＝28 cm，AC＝4 cm，点D是BC的中点，则线段AD＝　　     　cm；

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    探索勾股定理时，我们发现“用不同的方式表示同一图形的面积”可以解决线段和（或差）的有关问题，这种方法称为面积法。请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC,BD为腰AC上的高。

    (1)若BD=h，M时直线BC上的任意一点，M到AB、AC的距离分别为。

    ①　　 若M在线段BC上，请你结合图形①证明：= h；　　　　　　　　　　

    ②　　 当点M在BC的延长线上时，，h之间的关系为　　　　　 （请直接写出结论，不必证明）　　　　　　　　　　　　　　　　　　　　　　　　　

    （2）如图②，在平面直角坐标系中有两条直线：y = x + 6 ； ：y = -3x+6 若上的一点M到的距离是3，请你利用以上结论求解点M的坐标。

    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 图②


    查看答案和解析>>

    同步练习册答案