
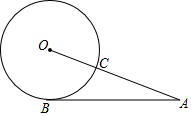
 如图,线段AB与⊙O相切于点B,线段AO与⊙O相交于点C,AB=12,AC=8,则⊙O的半径长为5.
如图,线段AB与⊙O相切于点B,线段AO与⊙O相交于点C,AB=12,AC=8,则⊙O的半径长为5. 科目:初中数学 来源: 题型:选择题
| A. | b>8 | B. | b>-8 | C. | b≥8 | D. | b≥-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
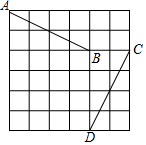 如图,A点的坐标为(-1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,-1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是(1,1)或(4,4).
如图,A点的坐标为(-1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐标为(3,-1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是(1,1)或(4,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
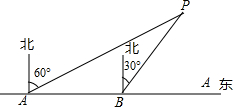 为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com