
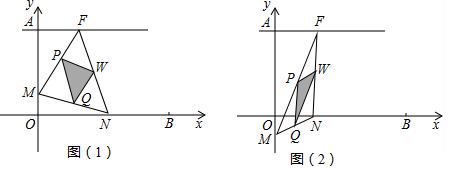
分析 (1)根据三角形中位线定理可得$\frac{PW}{MN}$=$\frac{WQ}{FM}$=$\frac{PQ}{FN}$=$\frac{1}{2}$,由此根据相似三角形的判定方法即可证明.
(2)分三种情形讨论)①如图2中,当∠MFN=90°,可得∠PQW=90°,作NK⊥AF于K.②如图3中,当∠FMN=90°,可得∠PWQ=90°.③如图4中,当∠MNF=90°时,可得∠QPW=90°,作FK⊥OB于K.分别利用相似三角形的性质,列出方程求解即可解决问题.
(3)构建二次函数,利用二次函数的性质即可解决问题.
解答 (1)证明:如图1中,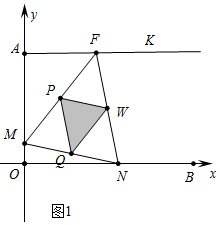
∵P、W、Q分别是FM、FN、MN的中点,
∴FN=2PQ,FM=2WQ,MN=2PW,
∴$\frac{PW}{MN}$=$\frac{WQ}{FM}$=$\frac{PQ}{FN}$,
∴△FMN∽△QWP
(2)①如图2中,当∠MFN=90°,可得∠PQW=90°,作NK⊥AF于K.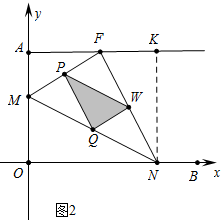
由△AMF∽△KFN,得$\frac{AM}{KF}$=$\frac{AF}{NK}$,
∴$\frac{x}{5-x}$=$\frac{3}{6}$,
∴x=$\frac{5}{3}$.
②如图3中,当∠FMN=90°,可得∠PWQ=90°.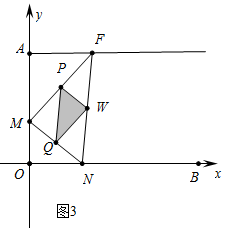
由△AMF∽△ONM,得$\frac{AM}{ON}$=$\frac{AF}{OM}$,
∴$\frac{x}{8-x}$=$\frac{3}{6-x}$,
整理得x2-9x+24=0,△<0,无解,这种情形不存在.
③如图4中,当∠MNF=90°时,可得∠QPW=90°,作FK⊥OB于K.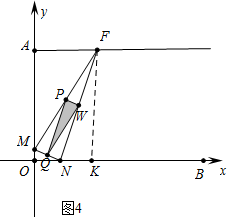
由△MON∽△NKF,得$\frac{OM}{NK}$=$\frac{ON}{KF}$,
∴$\frac{6-x}{x-5}$=$\frac{8-x}{3}$,
整理得x2-16x+58=0,解得x=8±$\sqrt{6}$都不符合题意舍弃.
综上所述,x=$\frac{5}{3}$时,△PWQ是直角三角形.
当△PQW不为直角三角形,x的取值范围0≤x<$\frac{5}{3}$或$\frac{5}{3}$<x≤6.
(3)在Rt△MON中,MN=$\sqrt{(6-x)^{2}+(8-x)^{2}}$=$\sqrt{2(x-7)^{2}+2}$,
∵2>0,
∴x=7时,MN有最小值为$\sqrt{2}$.
点评 本题考查相似综合题、相似三角形的判定和性质、直角三角形的判定和性质、二次函数等知识,解题的关键是学会分类讨论,学会构建二次函数,解决最值问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
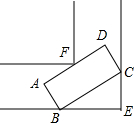 如图所示是一条宽为1.5m的直角走廊,现有一辆转动灵活的手推车,其矩形平板面ABCD的宽AB为l m,若要想顺利推过 (不可竖起来或侧翻) 直角走廊,平板车的长AD不能超过2.2m.(精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图所示是一条宽为1.5m的直角走廊,现有一辆转动灵活的手推车,其矩形平板面ABCD的宽AB为l m,若要想顺利推过 (不可竖起来或侧翻) 直角走廊,平板车的长AD不能超过2.2m.(精确到0.1,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com